Флуктуации числа молекул в объеме.

Рассмотрим флуктуации биномиального распределения. Для вычисления флуктуаций нам потребуется (см. пункт 3.4) знание среднего числа молекул 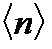 в выделенном объеме  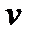и среднего значения квадрата .

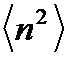Сосчитаем ещё раз среднее значение числа молекул 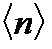 в объеме 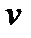, воспользовавшись красивым формальным приемом.

 

4.1. Среднее значение.

 

Запишем среднее значение 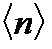 как произведение вероятности  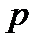на производную от функции распределения  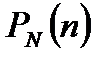по :

                                

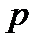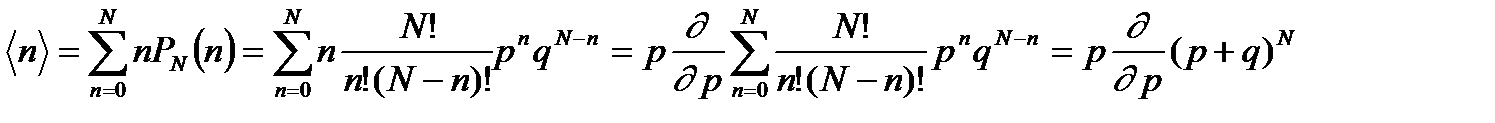.       (4.1)

После вычисления производной сделаем подстановку 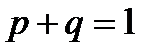, тогда

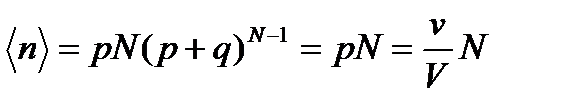                                                               .                                            (4.2)

Итак

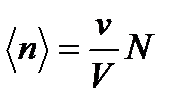                                                                               .                                                                         (4.3)

 

4.2. Относительная квадратичная флуктуация.

 

Для вычисления 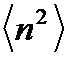 используем тот же формальный прием, что и в предыдущем пункте.

       

                                             .

 

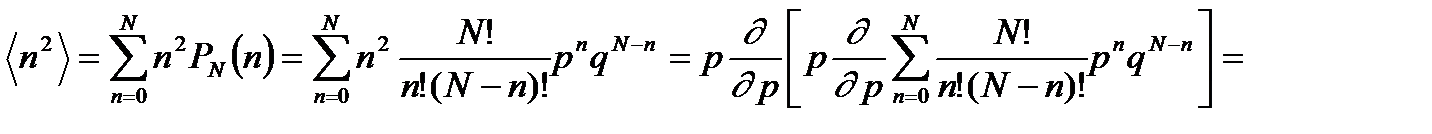
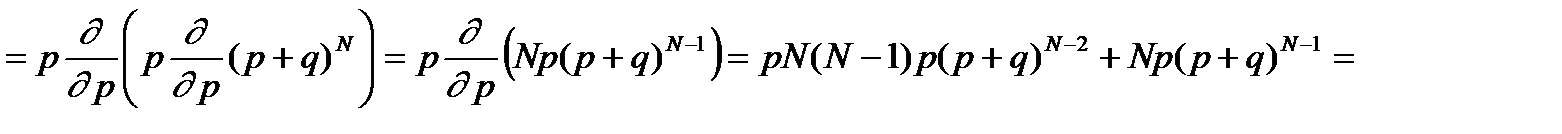
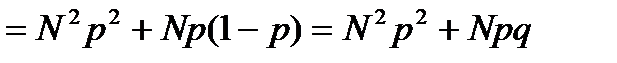Здесь мы опять воспользовались тем, что .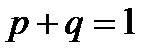

 Итак,

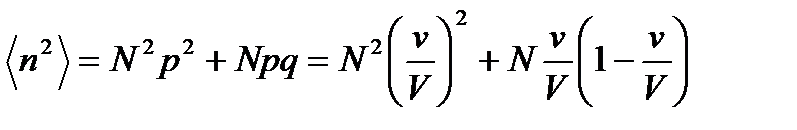                                             .                                  (4.4)

Сосчитаем теперь дисперсию:

                                .             (4.5)

Тогда для относительной квадратичной флуктуации получаем

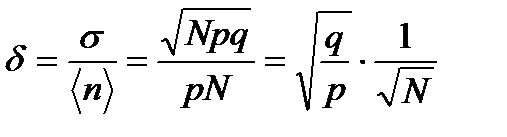                                                            .                                                     (4.6)

Важно, что относительная квадратичная флуктуация убывает с ростом числа частиц в системе:

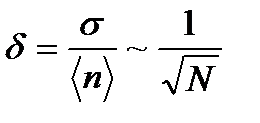                                                                       .                                                                           (4.7)

Физическое содержание полученного выражения очень важно. Исследуем его. Подставим в выражение для относительной квадратичной флуктуации 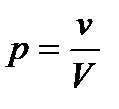 и :

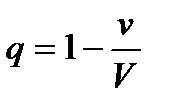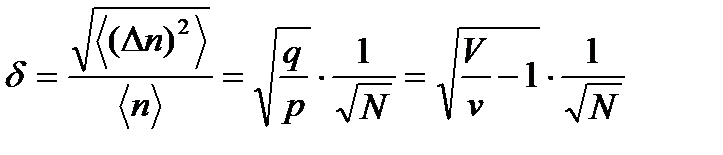                                                                                               (4.8)

1) Рассмотрим большой объем 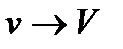, тогда относительная флуктуация стремится к нулю, т.к. число частиц в объеме  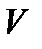фиксировано.

2) При уменьшении объема 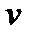 ( 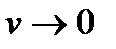) относительная флуктуация возрастает, т.е. при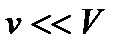

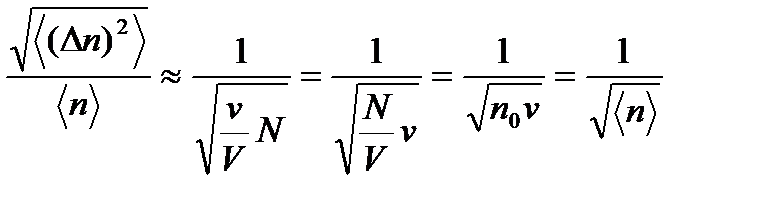                                         .                                        (4.9)

Очевидно, что с уменьшением области рассмотрения и, соответственно, 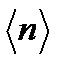 относительная флуктуация возрастает.

3). Пусть 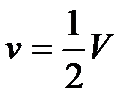, тогда .

 

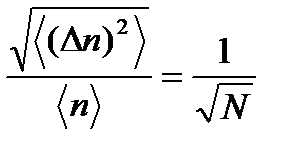Примеры: а) Пусть 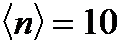 частиц и 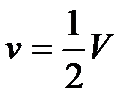, тогда относительная флуктуация

                                                                               

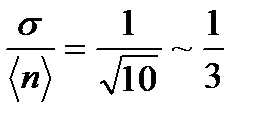
              б) Рассмотрим газ, находящийся при нормальных условиях в некотором объеме 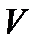. Средняя  

                  концентрация молекул в этом случае составляет 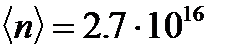 частиц/мм³. Даже для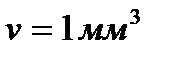  

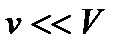                 ( ) получаем очень малую величину относительной квадратичной флуктуации:

                                                                      

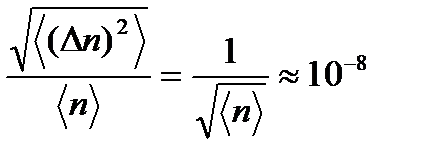
Полученный результат можно обобщить следующим образом. Относительная флуктуация всякой аддитивной величины убывает обратно пропорционально квадратному корню из числа частиц макроскопического тела, т.е. в макроскопических системах статистические флуктуации незначительны. Поэтому при достаточно большом числе частиц сама аддитивная величина может считаться практически постоянной во времени и с большой точностью равной своему среднему значению. Или иначе, подавляющую часть времени система находится в состояниях, в которых отклонения аддитивных параметров системы от среднего не превышают относительную флуктуацию.

Поэтому поведение системы большого числа частиц можно надежно описывать с помощью средних величин, характеризующих систему.

 

Распределения Пуассона и Гаусса.

 

Рассмотрим важные для статистики предельные случаи биноминального распределения.

Пусть 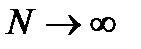,  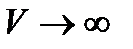и 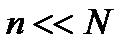 но так, что  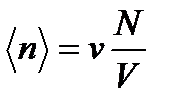остается постоянным.

Перепишем (3.15) в виде

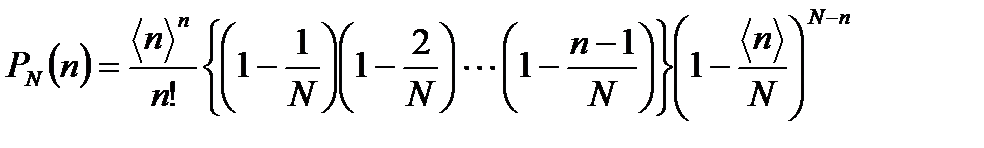                                          .               (3.16)

В силу 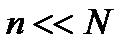 выражение, стоящее в фигурных скобках, мало отличается от единицы.

Учитывая далее, что

                                                                     ,

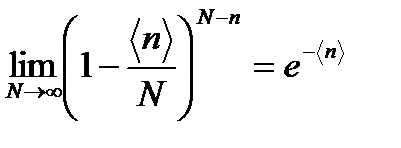получаем из (3.16) формулу Пуассона:

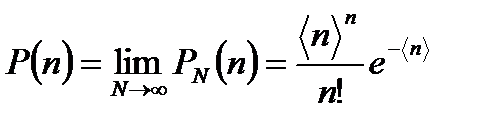                                                                     .                                             (3.17)

Заметим, что  удовлетворяет условию нормировки

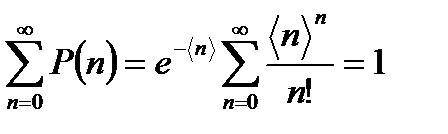                                                           ,                                                             (3.18)

так как сумма по 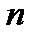 равна .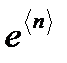

Рассмотрим формулу Пуассона в случае, когда 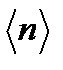,  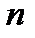и 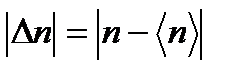 - большие числа, но .

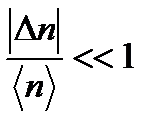Из (3.17) следует

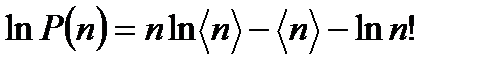                                                       .                                                             (3.19)

Преобразуя это выражение, воспользовавшись для 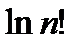 полной формулой Стирлинга

                                                              ,

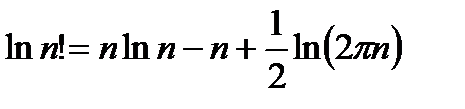и проведя дальнейшие преобразования, в результате получим распределение Гаусса:

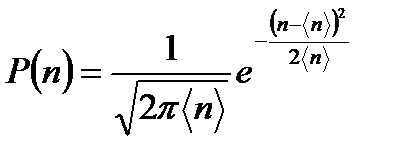                                                                .                                                             (3.21)

(Комментарии: БКФ, т.V, 321-327).

 

 

Системы и подсистемы. Квазизамкнутость. Статистическая независимость.

 

 

Систем, полностью удовлетворяющих термину “замкнутая”, т.е. не взаимодействующих ни с какими другими телами, вообще говоря, в природе не существует, за исключением, вероятно Вселенной.

Поэтому с практической точки зрения более интересными объектами являются малые, по сравнению со всей макроскопической системой, но в то же время содержащие очень большое число частиц, её части.                                                                                  

                                                                               Такие относительно малые, но в то же время    

                                                                         макроскопические части мы будем называть подсистемами.

                                                                         Подсистема опять есть механическая система, но уже не  

                                                                         замкнутая, а испытывающая всевозможные воздействия со

                                                                         стороны остальных частей системы. Из-за огромного числа

                                                                         степеней свободы окружающих подсистему остальных частей

                                                                         системы эти взаимодействия будут носить сложный и запутанный 

                                                                         характер. Поэтому весьма сложным и запутанным образом будет 

                                                                         меняться со временем и состояние рассматриваемой подсистемы.

                                                                                Однако эти малые части системы являются сами                            

                                                                         макроскопическими телами, поэтому мы можем считать, что в течение не слишком больших промежутков времени они ведут себя приблизительно как замкнутые системы.

Действительно, во взаимодействии подсистемы с окружающими частями участвуют преимущественно те частицы, которые находятся вблизи её поверхности. При этом относительное число этих частиц по сравнению с полным числом частиц в подсистеме быстро уменьшается с ростом её размеров. Поэтому при значительной величине подсистемы энергия взаимодействия с окружающими частями будет мала по сравнению с её внутренней энергией. О такой подсистеме можно сказать, что она является квазизамкнутой.

Можно провести следующие размерные оценки.

 

Объемная энергия подсистемы пропорциональна , где 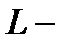 линейный размер, а  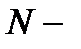число частиц в подсистеме.

Поверхностная энергия подсистемы пропорциональна .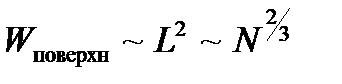

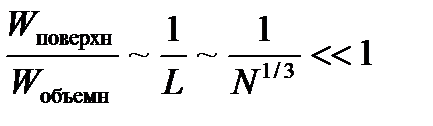                                                    , если  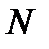велико.                                    (5.3)

 

Т.е. с увеличением числа частиц в подсистеме объемные эффекты растут значительно быстрее, чем поверхностные. И при достаточно большой подсистеме ее взаимодействие с окружающими частями будет мало по сравнению с внутренними взаимодействиями. Это справедливо и в том случае, когда взаимодействие между частицами мало (идеальный газ).

Тот важный факт, что различные подсистемы можно считать слабо взаимодействующими друг с другом, приводит к тому, что на протяжении указанных промежутков времени их можно считать независимыми также и в статистическом смысле.

Статистическая независимость означает, что состояние, в котором находится одна из подсистем, никак не влияет на вероятности различных состояний других подсистем.

 

Свойства статистического распределения для малых подсистем.

 

Статистическое распределение малой подсистемы не зависит

1) от начального состояния какой-либо другой малой части (подсистемы) той же системы, т.к. влияние этого начального состояния будет в течение времени 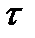 вытеснено влиянием остальных обширных частей макросистемы;

2) от начального состояния самой подсистемы, поскольку данная подсистема с течением времени проходит через все возможные состояния и каждое из них может быть выбрано в качестве начального.

.

 Очень важным является то, что практически все величины, описывающие физические свойства системы, могут рассматриваться как аддитивные. В частности, полная энергия системы может быть определена как

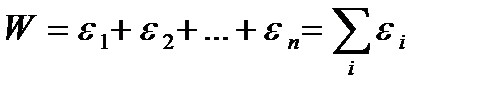                                                                                                        (5.4)

где 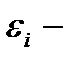 энергия квазизамкнутой подсистемы.

Если система замкнута и не взаимодействует ни с какими другими телами, то состояние системы можно характеризовать её полной энергией 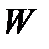, причем .

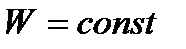Равенство (5.4) приблизительное, но выполняется с тем большей точностью, чем больше частиц содержится в системе и подсистемах. Действительно, как мы раньше выяснили, относительные флуктуации быстро падают с ростом числа частиц и малы при больших 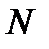, т.е. в течение достаточно большого промежутка времени физические величины мало отклоняются от своих средних значений.

     

Эти свойства макросистем дают возможность находить функцию распределения, не решая уравнения механики для этой системы с учетом начальных условий.

Если статистическое распределение для малой макроскопической подсистемы найдено, тогда можно вычислить вероятности различных значений любых величин, описывающих состояние рассматриваемой подсистемы

Важнейший результат этого рассмотрения: подсистему, входящую в замкнутую систему, и ее энергию можно рассматривать и описывать статистически. Это и есть вероятностное описание тепловых процессов.

 

5.3. Статистическое равновесие.

 

Если замкнутая макросистема находится в состоянии, в котором для каждой ее части (подсистемы), являющейся, самой по себе, макросистемой, значения физических величин, характеризующих состояние этой подсистемы, с большой точностью равны своим средним значениям, то говорят, что рассматриваемая система находится в состоянии статистического равновесия (о нем говорят также, как о термодинамическом или тепловом равновесии).

  Если замкнутая система наблюдается в течение достаточно большого промежутка времени, то подавляющую часть этого промежутка оно проводит в состоянии статистического равновесия.

  Если в какой-то начальный момент времени система не находилась в состоянии статистического равновесия (например, искусственно была выведена из него внешними воздействиями, а потом снова стала замкнутой), то в дальнейшем она обязательно перейдет в состояние статистического равновесия.

 Промежуток времени перехода в состояние статистического равновесия есть время релаксации. Переходные процессы изучает кинетика, а статистика изучает системы, находящиеся в состоянии статистического равновесия.

 

.       Заключая главу, ещё раз отметим, что основная задача статистической физики – вычисление на основе молекулярных представлений средних значений различных величин (давления, энергии, магнитного момента и др.) для макроскопических тел в состоянии статистического равновесия, а также флуктуаций соответствующих величин, относящихся к малым частям системы.

Предоставляя возможность вычислять средние значения величин, характеризующих макроскопические тела, статистика позволяет делать предсказания, оправдывающиеся с весьма большой степенью точности. В этом смысле предсказания статистической физики приобретают практически определенный, а не формально вероятностный характер

 

---

Дата добавления: 2022-07-01; просмотров: 100; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!