Емкость уединенной проводящей сферы
ЛЕКЦИЯ. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОИ ПОЛЕ.
Все тела в природе по их электрическим свойствам можно условно разделить на две большие категории — хорошо пропускающие электрический ток проводники и практически не пропускающие ток изоляторы (диэлектрики). Термин «диэлектрик» был введен М. Фарадеем. Деление веществ на проводники и диэлектрики по их способности проводить ток достаточно условно. В сильных электрических полях даже хорошие диэлектрики пропускают электрический ток.
Электрические свойства тел зависят от их внутреннего строения. Так, в металлах при обычных условиях имеется много «свободных» электронов, оторвавшихся от ионов кристаллической решетки и почти беспрепятственно перемещающихся по объему металла. В отсутствие внешних полей движение свободных электронов совершенно хаотично. Включение сколь угодно малого внешнего электрического поля вызывает направленное движение электронов. Такие вещества, в которых при обычных условиях имеется достаточно много «свободных» носителей заряда, называются проводниками.
Нас интересуют ответы на следующие вопросы. Что произойдет, если изолированному проводнику сообщить некоторый избыточный заряд? Что произойдет, если изолированный незаряженный проводник поместить во внешнее электрическое поле?
Если к проводнику добавить (отнять) часть электронов, то он заряжается отрицательно (положительно). Рассмотрим условия равновесия зарядов на проводнике. При равновесии зарядов их направленное движение внутри проводника отсутствует. Это означает, что поле внутри проводника равно нулю:  . В противном случае
. В противном случае  заряды должны были бы двигаться. Поскольку внутри проводника
заряды должны были бы двигаться. Поскольку внутри проводника  , то по теореме Остроградского-Гаусса в каждой точке объема образца
, то по теореме Остроградского-Гаусса в каждой точке объема образца  , поэтому объемная плотность зарядов внутри проводника также равна нулю
, поэтому объемная плотность зарядов внутри проводника также равна нулю  , а избыточные заряды могут быть расположены только на поверхности проводника. Это происходит потому, что одноименные заряды отталкиваются и стремятся расположиться как можно дальше друг от друга.
, а избыточные заряды могут быть расположены только на поверхности проводника. Это происходит потому, что одноименные заряды отталкиваются и стремятся расположиться как можно дальше друг от друга.
|
|
|
Ответим на вопрос: что будет, если в толще заряженного проводника имеется замкнутая внутренняя полость? Будут ли располагаться заряды также и на ее стенках? Исходя из качественных соображений, мы должны ответить отрицательно: заряды, отталкиваясь друг от друга, расположатся только на внешней поверхности проводника. К такому же выводу приводит теорема Остроградского — Гаусса. Если взять такую воображаемую поверхность, чтобы она целиком лежала в толще проводника и была бесконечно близка к стенкам полости, то во всех точках этой поверхности поле равно нулю, и, следовательно, равен нулю поток вектора электрической напряженности. Следовательно, на стенках полости зарядов нет.
|
|
|
Отсутствие поля внутри заряженного проводника означает постоянство потенциала внутри него: поскольку  , то
, то  . Таким образом, потенциал на поверхности проводника также постоянен и равен по величине потенциалу в объеме проводника. Следовательно, поверхность проводника эквипотенциальная (рис. 2.2).
. Таким образом, потенциал на поверхности проводника также постоянен и равен по величине потенциалу в объеме проводника. Следовательно, поверхность проводника эквипотенциальная (рис. 2.2).
Электрические заряды, располагающиеся на поверхности проводника с некоторой плотностью  , создают вне проводника электрическое поле. Вблизи поверхности проводника напряженность поля направлена по нормали
, создают вне проводника электрическое поле. Вблизи поверхности проводника напряженность поля направлена по нормали  в каждой точке поверхности, т. е.
в каждой точке поверхности, т. е.  так как эквипотенциальная поверхность перпендикулярна силовым линиям. Для вычисления поля вблизи проводника снова используем теорему Остроградского — Гаусса. В качестве воображаемой поверхности возьмем поверхность бесконечно малого цилиндра, расположенного перпендикулярно проводнику так, что одно из его оснований находится вне проводника, а другое — внутри (рис. 2.3).
так как эквипотенциальная поверхность перпендикулярна силовым линиям. Для вычисления поля вблизи проводника снова используем теорему Остроградского — Гаусса. В качестве воображаемой поверхности возьмем поверхность бесконечно малого цилиндра, расположенного перпендикулярно проводнику так, что одно из его оснований находится вне проводника, а другое — внутри (рис. 2.3).

Рис. 2.3. Электрическое поле вблизи поверхности изолированного заряженного проводника
В этом случае поток через основание внутри проводника равен нулю, так как внутри проводника нет поля. Далее, поток через боковые стенки также равен нулю, поскольку они параллельны вектору напряженности поля. Остается поток через основание площадью  вне проводника.
вне проводника.
|
|
|
Тогда полный поток вектора электрической напряженности  через поверхность цилиндра будет равен:
через поверхность цилиндра будет равен:

| (2.1) |
Согласно теореме Остроградского — Гаусса,

откуда

| (2.2) |
Таким образом, напряженность электрического поля вблизи поверхности заряженного проводника (с его внешней стороны) пропорциональна поверхностной плотности зарядов. Внутри проводника, напомним, поле равно нулю.
При внесении незаряженного проводника во внешнее электрическое поле свободные заряды начинают двигаться и через небольшое время приходят в равновесие. Создается стационарное распределение зарядов, при котором на одной стороне проводника образуется избыток отрицательных зарядов, а на другой — избыток положительных. Это явление называется электростатической индукцией (рис. 2.5).

Рис. 2.5. Электростатическая индукция
Поле индуцированных (появившихся на поверхности проводника) зарядов полностью компенсирует внутри проводника внешнее поле. В противном случае внутри проводника происходило бы движение электрических зарядов, и распределение не было бы стационарным. Итак, при равновесном состоянии суммарное поле (внешнее и индуцированных зарядов) внутри проводника равно нулю. Поэтому в отношении суммарного поля справедливы выводы, сделанные нами ранее для заряженных проводников в отсутствии внешнего поля.
|
|
|
В частности, электрическое поле будет отсутствовать во внутренней полости в материале проводника (рис. 2.6). На свойстве проводников экранировать внешние поля (не пропускать их внутрь области, окруженной проводником) основывается электростатическая защита от действия внешних электростатических полей (рис. 2.7).
Так, автомобиль является безопасным убежищем во время грозы, и не потому, что резина на колесах изолирует его от земли. Здесь мы должны быть благодарны теореме Остроградского — Гаусса. Однако следует подчеркнуть, что замкнутый полый проводник экранирует полость внутри себя только от внешних зарядов и полей. Если внести заряды внутрь полости, то там появится электрическое поле при том, что в самом проводнике поле, по-прежнему будет равно нулю.
Далее, суммарное поле вблизи проводника перпендикулярно его поверхности и равно

|
Рассмотрим следующую задачу. Дана сферическая металлическая оболочка с внутренним и внешним радиусами  и
и  соответственно. В центр полости помещен заряд
соответственно. В центр полости помещен заряд  . Найти электрическое поле и потенциал системы, а также распределение зарядов на поверхности оболочки (рис. 2.9).
. Найти электрическое поле и потенциал системы, а также распределение зарядов на поверхности оболочки (рис. 2.9).
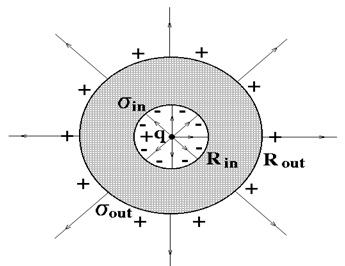
Рис. 2.9. Электрическое поле положительного заряда  окруженного металлической оболочкой
окруженного металлической оболочкой
Решение. Благодаря сферической симметрии заряды расположатся на поверхностях оболочки с постоянной поверхностной плотностью:  — на внутренней и
— на внутренней и  — на внешней сторонах. Рассмотрим сначала поле внутри оболочки. Проведем воображаемую сферическую поверхность радиусом
— на внешней сторонах. Рассмотрим сначала поле внутри оболочки. Проведем воображаемую сферическую поверхность радиусом  Внутри нее находится только заряд
Внутри нее находится только заряд  . Следовательно, поле в полости оболочки будет таким же, как и для изолированного заряда . Возьмем теперь поверхность радиусом
. Следовательно, поле в полости оболочки будет таким же, как и для изолированного заряда . Возьмем теперь поверхность радиусом  , где
, где  . Так как поле в металле отсутствует, равен нулю поток через нашу поверхность. Это значит, что полный заряд внутри нее равен нулю. Он складывается из заряда
. Так как поле в металле отсутствует, равен нулю поток через нашу поверхность. Это значит, что полный заряд внутри нее равен нулю. Он складывается из заряда  и полного заряда на внутренней поверхности, который, стало быть, равен
и полного заряда на внутренней поверхности, который, стало быть, равен  . С другой стороны, заряд на внутренней поверхности можно определить как
. С другой стороны, заряд на внутренней поверхности можно определить как  , откуда следует
, откуда следует  . Металлическая оболочка в целом была незаряженной, поэтому полный заряд
. Металлическая оболочка в целом была незаряженной, поэтому полный заряд  , появившийся на ее внутренней поверхности,
, появившийся на ее внутренней поверхности,
должен быть скомпенсирован полным зарядом  , возникшим на внешней поверхности оболочки (сохранение электрического заряда). Поэтому плотность заряда
, возникшим на внешней поверхности оболочки (сохранение электрического заряда). Поэтому плотность заряда  . Проведем наконец воображаемую поверхность вне металлической оболочки
. Проведем наконец воображаемую поверхность вне металлической оболочки  . Полный заряд внутри поверхности складывается из 1) заряда
. Полный заряд внутри поверхности складывается из 1) заряда  , 2) заряда
, 2) заряда  на внутренней поверхности оболочки и 3) заряда
на внутренней поверхности оболочки и 3) заряда  на ее внешней стороне. Поэтому внутри воображаемой поверхности находится заряд
на ее внешней стороне. Поэтому внутри воображаемой поверхности находится заряд  . Это значит, что электрическое поле вне оболочки снова совпадает с полем одиночного точечного заряда
. Это значит, что электрическое поле вне оболочки снова совпадает с полем одиночного точечного заряда  . Итак, мы установили, что электрическое поле направлено по радиус-вектору
. Итак, мы установили, что электрическое поле направлено по радиус-вектору  и по абсолютной величине равно
и по абсолютной величине равно

| (2.4) |
 Нам осталось найти потенциал поля в различных точках системы. Вне оболочки
Нам осталось найти потенциал поля в различных точках системы. Вне оболочки
потенциал совпадает с потенциалом точечного заряда:  На внешней поверхности оболочки потенциал равен
На внешней поверхности оболочки потенциал равен  Поскольку внутри оболочки поля нет, потенциал сохраняет это значение во всех точках внутри металла. Внутри полости потенциал опять совпадает с потенциалом точечного заряда. Поскольку последний определен с точностью до константы, имеем
Поскольку внутри оболочки поля нет, потенциал сохраняет это значение во всех точках внутри металла. Внутри полости потенциал опять совпадает с потенциалом точечного заряда. Поскольку последний определен с точностью до константы, имеем  Значение этого потенциала на внутренней поверхности оболочки
Значение этого потенциала на внутренней поверхности оболочки  должно совпасть со значением потенциала
должно совпасть со значением потенциала  на внешней оболочке. Отсюда можно найти постоянную
на внешней оболочке. Отсюда можно найти постоянную 

Рис. 2.10 Напряженность и потенциал электрического поля заряда q,
окруженного металлической оболочкой с внутренним радиусом Rin и внешним радиусом Rout. Пунктирные линии - характеристики поля заряда в отсутствие оболочки
Емкость уединенной проводящей сферы
Из предыдущего следует, что  . Величина С называется электроемкостью проводника. Рассмотрим сначала уединенный проводник (сферу),
. Величина С называется электроемкостью проводника. Рассмотрим сначала уединенный проводник (сферу),
| Уединенные проводники также обладают емкостью. Роль второй обкладки играют при этом бесконечно удаленные точки пространства. Рассмотрим, например, заряженную сферу радиусом | (2.6) | |
направленное вдоль радиуса. Потенциал, создаваемый заряженной сферой при  , дается выражением , дается выражением 
| (2.7) | |
Внутри проводящей сферы  , и, следовательно, потенциал во всех точках этой сферы постоянен и совпадает со значением потенциала на её поверхности:
, и, следовательно, потенциал во всех точках этой сферы постоянен и совпадает со значением потенциала на её поверхности:

| (2.8) |
Это значение в сущности является разностью потенциалов между поверхностью сферы и бесконечно удаленной точкой. По определению емкости

| (2.9) |
В СИ за единицу емкости принят фарад (в честь М. Фарадея): фарад это емкость такого проводника, которому для повышения потенциала на 1 В, необходимо сообщить заряд в 1 Кл:

Соотношение для емкости уединенной сферы в вакууме  показывает, что 1 Ф — это емкость шара с радиусом
показывает, что 1 Ф — это емкость шара с радиусом  м, что в 13 раз превышает радиус Солнца и в 1413 раз — радиус Земли. Таким образом, емкость Земли составляет примерно 1/1413 Ф, т. е.
м, что в 13 раз превышает радиус Солнца и в 1413 раз — радиус Земли. Таким образом, емкость Земли составляет примерно 1/1413 Ф, т. е.  мкФ. Иными словами, 1 Ф — это огромная емкость. Изготовлять конденсаторы такой емкости научились лишь относительно недавно, главным образом, благодаря совершенствованию технологии нанесения сверхтонких диэлектрических и металлических пленок.
мкФ. Иными словами, 1 Ф — это огромная емкость. Изготовлять конденсаторы такой емкости научились лишь относительно недавно, главным образом, благодаря совершенствованию технологии нанесения сверхтонких диэлектрических и металлических пленок.
Конденсаторы
Повышения емкости проводника можно достигнуть не только увеличением его размеров, но и за счет приближения к нему другого проводника. Примерами могут служить плоский конденсатор, сферический конденсатор и др. Мы вычислим их емкости, исходя из данных определений и геометрии конденсатора. Отношение  называется емкостью конденсатора.
называется емкостью конденсатора.
Плоский конденсатор
Идеальный плоский конденсатор представляет собой две металлические параллельные пластины, линейные размеры которых много больше расстояния  между ними. Пусть площадь каждой из пластин равна
между ними. Пусть площадь каждой из пластин равна  (рис. 2.12). На одну пластину помещен заряд
(рис. 2.12). На одну пластину помещен заряд  , на другую —
, на другую —  Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь «краевыми» эффектами — распределениями зарядов и конфигурациями полей вблизи их краев.
Если пластины достаточно велики, то их можно считать «бесконечными» в том смысле, что допустимо пренебречь «краевыми» эффектами — распределениями зарядов и конфигурациями полей вблизи их краев.
Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью. Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:
 Рис. 2.12. Электрическое поле идеального плоского конденсатора
Рис. 2.12. Электрическое поле идеального плоского конденсатора
Тогда заряды распределяются по внутренним поверхностям пластин практически равномерно, с постоянной плотностью  . Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:
. Разность потенциалов между обкладками равна интегралу от напряженности поля, взятому по любому пути между ними:

| (2.10) |
Поле, создаваемое двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями, является однородным, и его напряженность равна  (см. (2.3)).
(см. (2.3)).
Напряженность поля в пространстве, окружающем пластины, можно считать равной нулю, если пренебречь краевыми эффектами. Интегрируя вдоль силовой линии (которые ортогональны пластинам), получаем
|
| (2.11) | |
Отсюда находим емкость плоского конденсатора: 
| (2.12) | |
Цилиндрический конденсатор.
Цилиндрический конденсатор представляет собой два коаксиальных длинных проводящих цилиндра радиусами  и
и 
 и длиной
и длиной  . Предполагая, что
. Предполагая, что  , мы и в этом случае пренебрегаем краевыми эффектами. Линейная плотность заряда на цилиндрах равна
, мы и в этом случае пренебрегаем краевыми эффектами. Линейная плотность заряда на цилиндрах равна  . Мы уже вывели выражение для электрического поля длинного заряженного цилиндра (см. (1.17)):
. Мы уже вывели выражение для электрического поля длинного заряженного цилиндра (см. (1.17)):

| (2.13) |
Электрическое поле направлено по радиусу цилиндров. Интегрируя по этому пути от одной обкладки к другой, находим разность потенциалов между обкладками:

| (2.14) |
Отсюда следует выражение для емкости цилиндрического конденсатора:

| (2.15) |
В случае, когда зазор между обкладками  , можно использовать первый член разложения логарифма в ряд Тейлора
, можно использовать первый член разложения логарифма в ряд Тейлора

что приводит к выражению 
| (2.16) |
В скобках стоит произведение длины окружности цилиндра на его высоту, что равно площади поверхности цилиндра (площади обкладок). Т. о. мы воспроизвели в этом пределе выражение (2.12) для емкости плоского конденсатора.
Сферический конденсатор конденсатор.
Сферический конденсатор образуется двумя концентрическими сферами радиусами  и
и  . Интегрируя вдоль радиуса уже хорошо знакомое выражение
. Интегрируя вдоль радиуса уже хорошо знакомое выражение

получаем разность потенциалов между обкладками:

| (2.17) |
откуда

| (2.18) |
Если внешний радиус бесконечно велик  (физически это значит, что
(физически это значит, что  ), то вычитаемым в знаменателе можно пренебречь, и мы приходим к формуле (2.9) для емкости уединенной сферы. В обратном случае, когда
), то вычитаемым в знаменателе можно пренебречь, и мы приходим к формуле (2.9) для емкости уединенной сферы. В обратном случае, когда  зазор между обкладками можно положить в числителе
зазор между обкладками можно положить в числителе  Замечая, что
Замечая, что  есть площадь обкладок, мы снова приходим к формуле (2.12).
есть площадь обкладок, мы снова приходим к формуле (2.12).
Соединения конденсаторов
Последовательное соединение
Во многих случаях для получения нужной электроемкости конденсаторы объединяют в группу, которая называется батареей. Емкость батареи конденсаторов зависит от схемы соединения составляющих ее конденсаторов. Различают два вида соединения: последовательное и параллельное. Возможен также и смешанный тип соединения конденсаторов в батарею.
 Рис. 2.13. Последовательное соединение конденсаторов
Последовательное соединение. При зарядке батареи (рис. 2.13) разность потенциалов распределится между отдельными конденсаторами и будет равна
Рис. 2.13. Последовательное соединение конденсаторов
Последовательное соединение. При зарядке батареи (рис. 2.13) разность потенциалов распределится между отдельными конденсаторами и будет равна
Если первой обкладке батареи конденсаторов сообщается заряд Разности потенциалов
С другой стороны,
где
Для батареи из двух конденсаторов, например, отсюда следует выражение (рис. 2.14)
|

Рис. 2.14. Последовательное соединение двух конденсаторов
Параллельное соединение
 Рис. 2.15. Параллельное соединение конденсаторов
При параллельном соединении конденсаторов (рис. 2.15) разность потенциалов батареи равна разности потенциалов каждого отдельного конденсатора:
Рис. 2.15. Параллельное соединение конденсаторов
При параллельном соединении конденсаторов (рис. 2.15) разность потенциалов батареи равна разности потенциалов каждого отдельного конденсатора:
Заряжая такую батарею, мы сообщаем ей заряд, часть которого попадет на обкладки первого конденсатора, часть — на обкладки второго и т. д. Вследствие закона сохранения электрического заряда полный заряд батареи параллельно соединенных конденсаторов будет равен сумме зарядов отдельных конденсаторов:
Для каждого конденсатора можно написать соотношение
подставляя которое в (2.25), получим:
С другой стороны,
где
то есть при параллельном соединении конденсаторов емкость батареи равна сумме емкостей отдельных конденсаторов. Для батареи из двух конденсаторов, например, отсюда следует выражение (рис. 2.16)
Рис. 2.16. Параллельное соединение двух конденсаторов Задача. В сферический конденсатор с радиусами
Рис. 2.17. Сферический конденсатор с проводящей оболочкой внутри можно представить |
Решение. Емкость  прежнего конденсатора, чьими обкладками были сферы радиусами
прежнего конденсатора, чьими обкладками были сферы радиусами  дается формулой (2.18):
дается формулой (2.18):

Как видно из рисунка, новый конденсатор представляет собой последовательное соединение двух сферических конденсаторов: образованного сферами радиусами  (его емкость обозначим как
(его емкость обозначим как  ) и
) и  (его емкость будет
(его емкость будет  ). Имеем по той же формуле:
). Имеем по той же формуле:

| (2.30) |
Для емкости  последовательно соединенных конденсаторов получаем теперь
последовательно соединенных конденсаторов получаем теперь

Емкость нового конденсатора оказалась больше емкости первоначального.
Аналитическая формула для емкости такой батареи имеет вид:

| (2.31) |
При бесконечно тонкой внутренней сфере  заряды на ее поверхностях скомпенсируют друг друга, и мы должны получить формулу для емкости конденсатора
заряды на ее поверхностях скомпенсируют друг друга, и мы должны получить формулу для емкости конденсатора  без внутренней оболочки. Так оно и следует из формулы (2.31) при
без внутренней оболочки. Так оно и следует из формулы (2.31) при  . В обратном предельном случае, когда стенки внутренней оболочки близки к обкладкам первоначального конденсатора, получается формула для емкости двух последовательно соединенных плоских конденсаторов.
. В обратном предельном случае, когда стенки внутренней оболочки близки к обкладкам первоначального конденсатора, получается формула для емкости двух последовательно соединенных плоских конденсаторов.
Конденсаторы нашли широкое практическое применение, особенно в радиотехнике.
Энергия системы зарядов
Система заряженных тел обладает потенциальной энергией. Рассмотрим сначала два заряда  и
и  находящиеся на расстоянии
находящиеся на расстоянии  (рис. 2.19). При удалении одного из зарядов на бесконечность сила взаимодействия между ними уменьшается до нуля.
(рис. 2.19). При удалении одного из зарядов на бесконечность сила взаимодействия между ними уменьшается до нуля.

Рис. 2.19. К определению энергии системы электрических зарядов
Для сближения зарядов на расстояние  необходимо совершить работу, которая идет на изменение потенциальной энергии системы. Пусть заряд
необходимо совершить работу, которая идет на изменение потенциальной энергии системы. Пусть заряд  из бесконечности приближается к заряду
из бесконечности приближается к заряду  на расстояние
на расстояние  . Работа по его перемещению равна:
. Работа по его перемещению равна:

| (2.32) |
где  — потенциал поля, создаваемого зарядом
— потенциал поля, создаваемого зарядом  в той точке, в которую перемещается заряд
в той точке, в которую перемещается заряд  , т. е.
, т. е.

| (2.33) |
Аналогично, можно считать, что из бесконечно удаленной точки приближался заряд  :
:

| (2.34) |
Результаты оказались одинаковыми, поскольку одинаково конечное расположение зарядов. Следовательно, потенциальная энергия взаимодействия двух зарядов равна

| (2.35) |
или в симметричной форме

| (2.36) |
Теперь добавим к системе зарядов  и
и  третий заряд
третий заряд  (рис. 2.19), переносимый из бесконечности в точку, находящуюся от заряда
(рис. 2.19), переносимый из бесконечности в точку, находящуюся от заряда  на расстоянии
на расстоянии  и от заряда
и от заряда  на расстоянии
на расстоянии  . Соответствующая работа будет равна:
. Соответствующая работа будет равна:

| (2.37) |
где  — потенциал, создаваемый зарядами
— потенциал, создаваемый зарядами  и
и  в точке, где находится заряд
в точке, где находится заряд  .
.
Потенциальная энергия взаимодействия трех зарядов равна:

| (2.38) |
Перепишем полученное соотношение в виде:

| (2.39) |
или в симметричной форме

| (2.40) |
Ясно, что для произвольной системы зарядов имеем

| (2.41) |
где  — потенциал в точке, где находится заряд
— потенциал в точке, где находится заряд  , создаваемый всеми остальными зарядами, кроме
, создаваемый всеми остальными зарядами, кроме  .
.
Дата добавления: 2022-06-11; просмотров: 201; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 . Вне сферы
. Вне сферы  имеется кулоновское электрическое поле
имеется кулоновское электрическое поле


 ,
,  и т. д. могут быть не равны между собой, так как емкости отдельных конденсаторов, вообще говоря, неодинаковы. Поэтому разность потенциалов на клеммах всей батареи находится как сумма напряжений
и т. д. могут быть не равны между собой, так как емкости отдельных конденсаторов, вообще говоря, неодинаковы. Поэтому разность потенциалов на клеммах всей батареи находится как сумма напряжений  на каждом из конденсаторов:
на каждом из конденсаторов:

 емкость всей батареи. Следовательно, емкость батареи последовательно соединенных конденсаторов определяется выражением:
емкость всей батареи. Следовательно, емкость батареи последовательно соединенных конденсаторов определяется выражением:






 емкость всей батареи. Сравнивая (2.27) и (2.28) окончательно получаем
емкость всей батареи. Сравнивая (2.27) и (2.28) окончательно получаем


 см внутренней сферы и
см внутренней сферы и  см внешней сферы поместили сплошную сферическую проводящую оболочку с внутренним
см внешней сферы поместили сплошную сферическую проводящую оболочку с внутренним  см и внешним
см и внешним  см радиусами (рис. 2.17). Сравнить емкости прежнего и нового конденсаторов.
см радиусами (рис. 2.17). Сравнить емкости прежнего и нового конденсаторов.