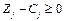Математична постановка ЦЗЛП.Геометрична інтерпретація розв ’ язків на площині.

Існує доволі широкий клас задач математичного програмування, в економіко-математичних моделях яких одна або кілька змінних мають набувати цілих значень, наприклад, коли йдеться про кількість верстатів у цеху, корів у сільськогосподарських підприємствах тощо, тобто коли така вимога випливає з особливостей технології виробництва. До цілочислового програмування належать також задачі оптимізації, в яких змінні набувають лише двох значень — 0 або 1 (бульові, або бінарні, змінні).

Розглянемо приклад. Інвестиційна компанія може вкласти кошти у три різні підприємства. Ефективність кожного проекту оцінено згідно з тим, що його реалізація можлива за чотирьох умов. Дані про ці проекти наведено в таблиці:

Проект	Змінна	Умови реалізації проектів
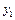
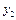
1		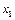8	15	21	4
2		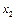10	16	18	6
3		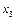12	14	17	7
Імовірності оцінки реалізації проектів		0,2	0,1	0,4	0,3

 

Кожна змінна 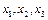 може набувати лише двох значень -1 або 0, тобто інвестиційна компанія вкладає або не вкладає кошти у відповідне підприємство.

До цілочислового програмування відносять задачі про призначення, найкоротший шлях і т. ін. У реальних задачах часто цілочислових значень набувають не всі, а одна чи кілька змінних. Такі задачі називають частково цілочисловими.

Загальна задача цілочислового програмування записується так:

(6.1)

за умов

	(6.2)
	(6.3)
	(6.4)

 

Для знаходження оптимального розв'язку цілочислових задач застосовують спеціальні методи. Найпростішим методом розв'язування цілочислової задачі є знаходження її оптимального розв'язку як задачі, що має лише неперервні змінні, з подальшим округленням останніх. Такий підхід часто є виправданим. Нехай, наприклад, у результаті розв'язування задачі про поєднання галузей у сільськогосподарському підприємстві дістали, що воно по требує 1235,6 корів. Округливши це значення корів до 1236, не припустимося значної похибки. Проте в деяких випадках такі спрощення призводять до істотних неточностей. Якщо, скажімо, у разі розв'язування як неперервної задачі про сушильний цех, що може бути обладнаний агрегатами трьох типів, дістали , будь-які округлення недопустимі.

Для знаходження оптимальних планів задач цілочислового програмування застосовують дві основні групи методів:

· методи відтинання;

· комбінаторні методи.

Основою методів відтинання є ідея поступового «звуження» області допустимих розв'язків розглядуваної задачі. Пошук ціло числового оптимуму починається з розв'язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисловість змінних, многокутник допустимих розв'язків послабленої задачі поступово зменшуємо доти, доки змінні оптимального розв'язку не набудуть цілочислових значень.

До цієї групи належать:

   а) методи розв'язування повністю цілочислових задач (дробовий алгоритм Гоморі);

   б) методи розв'язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).

Комбінаторні методи цілочислової оптимізації базуються на повному переборі всіх допустимих цілочислових розв'язків, тобто вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається лише частина розв'язків (досить невелика), а решта враховується одним зі спеціальних методів.

Найпоширенішим у цій групі методів є метод віток і меж.

Починаючи з розв'язування послабленої задачі, він передбачає розбиття початкової задачі на дві підзадачі виключенням областей, що не мають цілочислових розв'язків, і дослідженням кожної окремої частини многокутника допустимих розв'язків.

Для розв'язування задач із бульовими змінними застосовують комбіновані методи, причому оскільки змінні є бульовими, то методи пошуку оптимуму значно спрощуються.

 

Метод Гоморі

Нехай маємо задачу цілочислового програмування (6.1)— (6.4). Для її розв'язування можна скористатися ітеративним методом Гоморі. Суть його полягає ось у чому:

       1. Знаходять розв'язок послабленої, тобто задачі без вимог цілочисловості змінних — (6.1)—(6.3).

Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є оптимальним планом задачі цілочислового програмування (6.1)—(6.4).

       2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:

де символ {} позначає дробову частину числа.

Для визначення дробової частини будь-якого числа від цього числа віднімають цілу його частину — найбільше ціле число, що не перевищує даного. Цілу частину числа позначають символом []. Наприклад,

[1,3] = 1; [-1,3] = -2; {1,3} = 1,3 - 1 = 0,3; {-1,3} = -1,3 - (-2) =2 - 1,3 = 0,7.

3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Здобуту розширену задачу розв'язують, а далі перевіряють її розв'язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв'язку або доведено, що задача не має допустимих розв'язків у множині цілих чисел.

Досвід показує, що процес розв'язування задач великої розмірності методом Гоморі повільно збіжний. Істотними є також похибки округлення, які можуть призвести до того, що отриманий цілочисловий план не буде оптимальним.

Задача 6.1. Сільськогосподарське підприємство задумало створити сушильний цех на виробничій площі 190м², маючи для цього 100 тис.грн. і можливість придбати устаткування двох типів А і В. Техніко-економічну інформацію про ці два види устаткування подано в таблиці:

 

Техніко-економічний показник	Устаткування		Ресурс
	А	В
Вартість, тис. грн.	25	10	100
Необхідна виробнича площа, м2	40	20	190
Потужність, тис. грн./рік	350	150	-

 

Розв'язування. Нехай 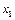 і 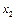 — кількість комплектів устатку вання відповідно типу А і В.

Запишемо економіко-математичну модель:

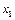і 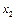 - цілі.

Розв'язуємо задачу, нехтуючи умовою цілочисловості. Остання симплексна таблиця набере вигляду:

		План	350	150	0	0
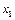
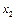
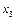
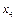
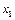
	350	1	1	0
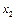
	150		0	1
		1475	0	0	10

 

Значення другої змінної є дробовим числом, що не задовольняє початкові умови задачі. Побудуємо для другого рядка наведеної симплексної таблиці додаткове обмеження виду

        Оскільки  то додаткове обмеження набирає вигляду

        Зведемо його до канонічної форми та введемо штучну змінну:

Приєднавши здобуте обмеження до останньої симплексної таблиці з умовно-оптимальним планом, дістанемо:

		План	350	150	0	0	0	- М
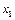
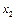
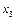
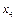
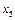
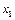
	350	1	1	0			0	0
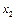
	150		0	1			0	0
	- М		0	0			-1	1
		1475	0	0	10		0	0
		М	0	0	М	М	М	0

 

Розв'язуючи наведену задачу, остаточно знаходимо цілочисловий оптимальний план:

.

Метод «віток і меж»

Ефективнішим за метод Гоморі розв'язування задач цілочислового програмування є метод «віток і меж». Спочатку, як і в разі методу Гоморі, розв'язується послаблена (відкиданням умови цілочисловості) задача.

           З цією метою застосовується симплексний метод.

 Нехай потрібно знайти 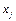 — цілочислову змінну, значення якої  в оптимальному плані послабленої задачі є дробовим. Тоді можна стверджувати, що в інтервалі  цілих значень немає.

Наприклад, якщо , дістаємо інтервал (2,3), де, очевидно, немає 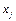 яке набуває цілого значення.

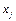Значенню  відповідає інтервал (-3; -2), де також не існує цілого значення . Отже, допустиме ціле значення  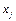має задовольняти одну з нерівностей

або .

Приписавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві не пов'язані між собою задачі. Тобто початкову задачу цілочислового програмування (6.1)—(6.4) розіб'ємо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв'язуватимемо дві такі задачі:

(6.5)

за умов

	(6.6)
	(6.7)
	(6.8)
	(6.9)
	(6.10)

за умов

	(6.11)
	(6.12)
	(6.13)
	(6.14)

 

де  —компонент розв'язку задачі (6.1)—(6.4).

Далі симплекс-методом розв'язуємо послаблені задачі (6.6)— (6.9) і (6.10)—(6.14), тобто з відкиданням обмежень (6.8) і (6.13). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв'язками задачі (6.1)—(6.4). Інакше пошук розв'язку задачі триває. Для подальшого розгалуження беремо задачу з найбільшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з найменшим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв'язку. Здобутий план — оптимальний.

Розв'язування цілочислових задач методом «віток і меж» можна значно прискорити, приєднавши обмеження виду (6.9) і (6.14) до останньої симплекс-таблиці не початкової (6.1)—(6.4), а відповідних задач.

Розв'яжемо методом «віток і меж» задачу 6.1.

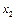Відкинувши умову цілочисловості, дістанемо розв'язок . Отже, допустиме ціле значення  має задовольняти одну з нерівностей  або . Далі приєднуємо до задачі кожне з обмежень, нехтуючи умовою цілочислово сті, і розв'язуємо по черзі обидві утворені задачі. Для першої (з обмеженням ) оптимальним буде розв'язок , а для другої (з обмеженням ) — розв'язок  . Оскільки цілочислового плану не знайдено, процес необхідно продовжити, узявши для наступного розгалуження першу задачу, оптимальний план якої дає більше значення функціоналу. Далі розв'язуємо задачу, приєднуючи до неї обмеження , звідки й знаходимо оптимальний план , що збігається з розв'язком, здобутим за методом Гоморі.

 

---

Дата добавления: 2022-01-22; просмотров: 17; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!