СОДЕРЖАЩИХ КВАДРАТНЫЙ ТРЕХЧЛЕН
Интеграл 
находится путем выделения полного квадрата из квадратного трехчлена, стоящего в знаменателе. В результате получается табличный интеграл 
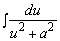или 
.
Интеграл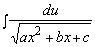 
аналогичными действиями сводится к табличным 
или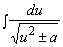 
.
Для нахождения интеграла 
необходимо выделить в числителе дроби дифференциал знаменателя и разложить полученный интеграл на сумму двух интегралов: первый из них сводится к виду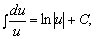 
где 
, а второй интеграл вида .
Для нахождения интеграла 
следует также в числителе дроби выделить дифференциал подкоренного выражения и разложить интеграл на сумму двух: первый сводится к интегралу от степенной функции вида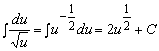 
, где 
, а второй интеграл - это интеграл вида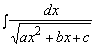 
.
11. Интегрирование дробно-рациональных функций.
12. Интегрирование иррациональных функций.
13. Интегрирование тригонометрических функций.
14. Задачи, приводящие к понятию определенного интеграла.
15. Интегральная сумма. Определение определенного интеграла. Теорема существования определенного интеграла.
А) 
Б) 
В) 
16. Свойства определенного интеграла.
17. Формулы среднего значения определенного интеграла.
18. Теорема о существовании первообразной для непрерывной на интервале функции.
19. Формула Ньютона-Лейбница вычисления определенного интеграла.
20. Замена переменной под знаком определенного интеграла.
21. Методы приближенного вычисления определенного интеграла.
22. Интегрирование по частям определенного интеграла.
23. Несобственные интегралы 1-ого рода. Определение. Вычисление. Простой признак сравнения
24. Несобственные интегралы 1-ого рода. Предельный признак сравнения.
25. Несобственные интегралы 2-ого рода.
26. Применение определенного интеграла к вычислению площадей плоских фигур.
27. Применение определенного интеграла к вычислению длины дуги.
28. Применение определенного интеграла к вычислению объема тела по площадям параллельных сечений, объема тела вращения. Площадь плоской фигуры в декартовых координатах; Площадь плоской фигуры в полярных координатах.
А)
Б)
В) 
29. Применение определенного интеграла к вычислению центра масс тел и моментов инерции тел.
30. Применение определенного интеграла для решения физических и технических задач.
31. Окрестность точки. Замкнутые и открытые множества. Области
При задании математического пространства определяется функция его отображения на физическое пространство, называемое в дальнейшем областью отображения, или просто областью.
Область – это рабочее поле, выделяемое в пределах страницы с некоторой другой, удобной для пользователя системой координат. В частности, при задании страницы ее поле автоматически определяется как область, совпадающая со страницей.
32. Способы задания ФНП. Линии уровня.
33. Предел и непрерывность ФНП.
34. Частные производные ФНП.
35. Дифференцируемость ФНП, дифференциал ФНП.
39. Дифференциал сложной функции нескольких переменных.
40. Производные и дифференциалы высших порядков.
41. Дифференцирование неявно заданных функций.
42. Необходимые условия экстремума функции двух переменных. Экстремумы
+ 43
43. Достаточные условия экстремума функции двух переменных
45. Достаточные условия экстремума ФНП, выраженные через второй дифференциал.
46. Комплексные числа. Понятия модуля и аргумента комплексных чисел. Формы представления комплексного числа. Математические действия над комплексными числами.
А) 
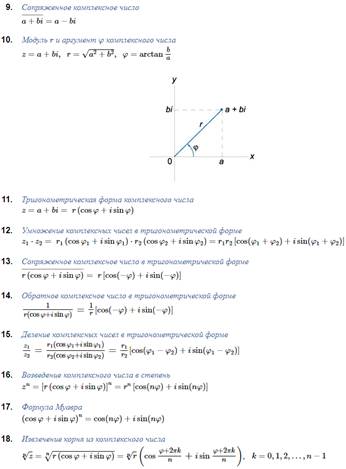
Б)
В)
Г) 
Дата добавления: 2021-07-19; просмотров: 48; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!