Кинематика вращательного движения твердого тела
Модуль 1.1
ГЛАВА 1 Кинематика
Механика – это раздел физики, в котором изучается движение тел в пространстве и во времени.
Тело или система тел, относительно которых определяется положением изучаемых тел, называется телом отсчета.
Совокупность тел отсчета, т.е. пространственных ориентиров и измерителя времени (часов) образует систему отсчета.
В качестве системы отсчета можно взять декартову систему координат  ,
,  ,
,  , задаваемую ортами (единичными векторами)
, задаваемую ортами (единичными векторами)  ,
,  ,
,  (рис. 1.1).
(рис. 1.1).
Рис. 1.1

Среди всевозможных систем отсчета выделяются такие, в которых тела, не подверженные воздействию других тел, сохраняют состояние покоя или равномерного прямолинейного движения. Эти особенные системы отсчета называются инерциальными. Существование инерциальных систем установлено из опыта и представляет собой закон природы.
Системы отчета, движущиеся с ускорением относительно инерциальных систем, называются неинерциальными.
Кинематика материальной точки
Существует три способа описания движения точки: векторный, координатный и естественный. Рассмотрим их последовательно.
Векторный способ Положение интересующей нас точки  задают радиус - вектором
задают радиус - вектором  - вектором, проведенным из начала координат в данную точку. При движении точки
- вектором, проведенным из начала координат в данную точку. При движении точки  ее радиус – вектор меняется как по модулю, так и по направлению, т.е.
ее радиус – вектор меняется как по модулю, так и по направлению, т.е.  зависит от времени
зависит от времени  .
.
|
|
|
Рис. 1.2
Траекторией точки называют геометрическое место концов радиус – вектора  .
.
Пусть за промежуток времени  точка
точка  переместилась из точки 1 в точку 2 (рис.1.2). Вектор перемещения
переместилась из точки 1 в точку 2 (рис.1.2). Вектор перемещения  точки
точки  представляет собой приращение радиус – вектора
представляет собой приращение радиус – вектора  за время
за время  :
:  . Средний вектор скорости
. Средний вектор скорости  за время
за время  равен
равен
 (1.1)
(1.1)
Вектор  совпадает по направлению с
совпадает по направлению с  .
.
Вектор скорости  точки в данный момент времени определяется как предел отношения
точки в данный момент времени определяется как предел отношения  при
при  , т.е.
, т.е.
 . (1.2)
. (1.2)
Это значит, что вектор скорости  точки в данный момент времени равен производной от радиуса – вектора
точки в данный момент времени равен производной от радиуса – вектора  по времени и направлен по касательной к траектории в данной точке в сторону движения точки
по времени и направлен по касательной к траектории в данной точке в сторону движения точки  .
.
Из рис.1.2 видно, что путь  , пройденный частицей за
, пройденный частицей за  в общем случае не равен
в общем случае не равен  , но отношение
, но отношение  при уменьшении
при уменьшении  стремится к единице, т.е.
стремится к единице, т.е.  .
.
Поэтому модуль вектора  равен
равен  или
или  .
.
 . (1.3)
. (1.3)
|
|
|
Движение точки характеризуется также ускорением. Вектор ускорения  определяет скорость изменения вектора скорости точки со временем:
определяет скорость изменения вектора скорости точки со временем:
 , (1.4)
, (1.4)
или учитывая (1.2), можно написать, что  (1.5)
(1.5)
Следовательно, ускорение равно первой производной скорости по времени либо второй производной радиус – вектора по времени.
Таким образом, зная зависимость  , можно найти
, можно найти  и
и  .
.
Возникает и обратная задача: можно ли найти  и
и  , зная зависимость
, зная зависимость  ?
?
Оказывается, для получения однозначного решения этой задачи необходимо еще знать начальные условия, а именно  и
и  .
.
Рассмотрим простейший случай, когда в процессе движения  , т.е. случай равнопеременного прямолинейного движения.
, т.е. случай равнопеременного прямолинейного движения.
Согласно (1.4)  , тогда
, тогда
 , но
, но  ,
,
тогда  .
.
Согласно (1.2)  , тогда
, тогда
 .
.
Учитывая, что  , получим
, получим
 .
.
В заключение напомним, что в СИ размерности равны:  = м,
= м,  = м/с,
= м/с,  = м/с2.
= м/с2.
Координатный способ
В этом способе с выбранным телом отсчета жестко связывают определенную систему координат (декартовую, полярную, криволинейную и т.д.).
|
|
|
Рис.1.3
Ограничимся декартовой системой координат  ,
,  ,
,  (рис.1.1). Изобразим радиус – вектор
(рис.1.1). Изобразим радиус – вектор  в этой системе координат (рис.1.3).
в этой системе координат (рис.1.3).
Запишем вектор  , используя орты
, используя орты  ,
,  ,
,  :
:
 , (1.6)
, (1.6)
где  - проекции вектора
- проекции вектора  на координатные оси (также функции времени).
на координатные оси (также функции времени).
Вектор скорости равен
 . (1.7)
. (1.7)
Здесь  ,
,  ,
,  - компоненты скорости, т.е. проекции вектора
- компоненты скорости, т.е. проекции вектора  на координатные оси.
на координатные оси.
Таким образом,
 . (1.8)
. (1.8)
Модуль вектора скорости равен
 (1.9)
(1.9)
Направление вектора  задается направляющими косинусами по формулам
задается направляющими косинусами по формулам
 ,
,  ,
,  , (1.10)
, (1.10)
где  - углы между вектором
- углы между вектором  и осями
и осями  соответственно.
соответственно.
Дифференцируя формулу (1.7) по времени, получим выражение для ускорения
 , (1.11)
, (1.11)
где  ,
,  ,
,  – компоненты ускорения, т.е. проекции вектора
– компоненты ускорения, т.е. проекции вектора  на координатные оси.
на координатные оси.
|
|
|
Модуль вектора ускорения  и его направление определяется аналогичными формулами (1.9) и (1.10).
и его направление определяется аналогичными формулами (1.9) и (1.10).
Таким образом, зная зависимость координат от времени  ,
,  ,
,  – закон движения точки, можно найти
– закон движения точки, можно найти  ,
,  ,
,  , а также решить ряд других вопросов: найти траекторию точки, зависимость пройденного пути
, а также решить ряд других вопросов: найти траекторию точки, зависимость пройденного пути  от времени, зависимость скорости от положения точки и т.д.
от времени, зависимость скорости от положения точки и т.д.
Например, зная модуль скорости  , можно вычислить путь, пройденный частицей от момента времени
, можно вычислить путь, пройденный частицей от момента времени  до момента времени
до момента времени  . Согласно (1.3)
. Согласно (1.3)  . Проинтегрировав это выражение по времени от
. Проинтегрировав это выражение по времени от  до
до  , найдем путь
, найдем путь  за это время:
за это время:
 . (1.12)
. (1.12)
«Естественный» способ
Этот способ применяют тогда, когда траектория точки известна заранее. Положение точки  задается дуговой координатой
задается дуговой координатой  - расстоянием вдоль траектории от выбранного начала отсчета
- расстоянием вдоль траектории от выбранного начала отсчета  (рис.1.4).
(рис.1.4).
Скорость точки Введем единичный вектор  , связанный с движущейся точкой
, связанный с движущейся точкой  и направленный по касательной к траектории.
и направленный по касательной к траектории.
Вектор скорости  направлен по касательной к траектории, поэтому
направлен по касательной к траектории, поэтому
 , (1.13)
, (1.13)
где  - модуль вектора скорости.
- модуль вектора скорости.
Рис.1.4
Ускорение точки Изменение вектора скорости  может происходить как по величине, та и по направлению, поэтому, продифференцировав (1.13) по времени, будем иметь в выражении для ускорения два слагаемых:
может происходить как по величине, та и по направлению, поэтому, продифференцировав (1.13) по времени, будем иметь в выражении для ускорения два слагаемых:
 . (1.14)
. (1.14)
Затем преобразуем второе слагаемое:
 . (1.15)
. (1.15)
Определим приращение вектора  на участке
на участке  (рис.1.5), учитывая, что
(рис.1.5), учитывая, что  = 1.
= 1.
Как видно из рис.1.5, угол
 , откуда
, откуда  , причем при
, причем при  и
и  . Здесь
. Здесь  - радиус кривизны траектории в данной точке 1,
- радиус кривизны траектории в данной точке 1,  - центр кривизны.
- центр кривизны.
Рис. 1.5
Введя единичный вектор  нормали траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде:
нормали траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде:
 . (1.16)
. (1.16)
Подставим (1.16) в (1.15) и полученное выражение в (1.14).
В результате найдем
 , или (1.17)
, или (1.17)
 ,
,
где
 - называют тангенциальным (т.е. касательным) ускорением, оно характеризует быстроту изменения модуля скорости,
- называют тангенциальным (т.е. касательным) ускорением, оно характеризует быстроту изменения модуля скорости,
 - называют нормальным ускорением, оно характеризует быстроту изменения направления скорости.
- называют нормальным ускорением, оно характеризует быстроту изменения направления скорости.
Таким образом, полное ускорение  точки может быть представлено как векторная сумма тангенциального и нормального ускорения.
точки может быть представлено как векторная сумма тангенциального и нормального ускорения.
Модуль полного ускорения точки
 . (1.18)
. (1.18)
Кинематика вращательного движения твердого тела
При вращении твердого тела все его точки движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.
Пусть за время  тело поворачивается на угол
тело поворачивается на угол  , тогда средняя угловая скорость равна
, тогда средняя угловая скорость равна
 . (1.19)
. (1.19)
Мгновенное значение угловой скорости определяется выражением
 . (1.20)
. (1.20)
Единицей угловой скорости служит радиан в секунду (рад/с).
Рис.1.6
Чтобы охарактеризовать не только быстроту вращения, но также и ориентацию оси вращения в пространстве и направление вращения, вводят векторную величину угловой скорости  .
.
Направлен вектор  вдоль оси вращения, причем так, что направление вращения и направление
вдоль оси вращения, причем так, что направление вращения и направление  образуют правовинтовую систему (т.е. связаны правилом буравчика) (рис. 1.6). Так как направление угловой скорости определяется условно,
образуют правовинтовую систему (т.е. связаны правилом буравчика) (рис. 1.6). Так как направление угловой скорости определяется условно,  является псевдовектором.
является псевдовектором.
Изменение угловой скорости со временем характеризуется векторной величиной
 , (1.21)
, (1.21)
которая называется угловым ускорением.
Причем если вращение вокруг неподвижной оси ускоренное, векторы  и
и  направлены в одну и ту же сторону, если вращение замедленное, то в противоположенные стороны.
направлены в одну и ту же сторону, если вращение замедленное, то в противоположенные стороны.
Единицей углового ускорения в СИ является радиан на секунду в квадрате (рад/с2).
Модуль углового ускорения равен
 (1.22)
(1.22)
Проекция углового ускорения на направление угловой скорости определяется формулой:
 , (1.23)
, (1.23)
и может быть как положительной, так и отрицательной.
Связь между линейными и угловыми величинами Найдем связь векторов  и
и  с величинами
с величинами  и
и  , которые называют линейными скоростью и ускорением.
, которые называют линейными скоростью и ускорением.
Рис. 1.7
Из рис. 1.7 видно, что точка тела, находящаяся на расстоянии  от оси вращения, при повороте тела на угол
от оси вращения, при повороте тела на угол  проходит путь
проходит путь  . Тогда модуль линейной скорости точки равен:
. Тогда модуль линейной скорости точки равен:
 .
.
Таким образом, связь между величинами линейной и угловой скорости:
 . (1.24)
. (1.24)
Будем определять положение точек тела с помощью радиус – вектора  , проведенного из точки
, проведенного из точки  , лежащей на оси вращения. Из рис. 1.7 видно, что
, лежащей на оси вращения. Из рис. 1.7 видно, что  , тогда
, тогда  . Отсюда следует, что
. Отсюда следует, что
 (1.25)
(1.25)
Модуль нормального ускорения определяется формулой
 (1.26)
(1.26)
Модуль тангенциального ускорения
 (1.27)
(1.27)
Отсюда модуль полного ускорения
 (1.28)
(1.28)
Задачи
Задача 1 Точка  движется по дуге радиусом
движется по дуге радиусом  (рис.1.8). Ее скорость
(рис.1.8). Ее скорость  зависит от дуговой координаты
зависит от дуговой координаты  по закону
по закону  , где
, где  - постоянная. Найдем угол
- постоянная. Найдем угол  между векторами полного ускорения
между векторами полного ускорения  и скорости точки
и скорости точки  как функцию координаты
как функцию координаты  .
.
Решение
Рис. 1.8
Из рис.1.8 видно, что  , где
, где
 .
.
Учитывая, что  , получим
, получим
 .
.
Нормальное ускорение

В результате 
Задача 2 Компоненты скорости материальной точки определяются выражениями:  ,
,  ,
,  (множители при
(множители при  выражены в м/с2). Найти ускорение точки и его модуль.
выражены в м/с2). Найти ускорение точки и его модуль.
Решение
Компоненты ускорения равны производным по времени компонент скорости
 м/с2,
м/с2, 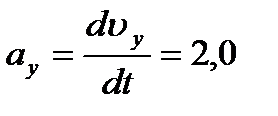 м/с2,
м/с2,  м/с2.
м/с2.
Вектор равен  , тогда в нашем случае
, тогда в нашем случае  .
.
Квадрат модуля вектора равен сумме квадратов его компонент  .
.
Поэтому  м/с2.
м/с2.
Задача 3 Модуль скорости материальной точки изменяется со временем по закону  , где
, где  = 1,0 м/с3. Найти путь, пройденный точкой за первые 10,0 с движения.
= 1,0 м/с3. Найти путь, пройденный точкой за первые 10,0 с движения.
Решение
Путь равен определенному интегралу от модуля скорости по времени:
 м.
м.
Задача 4 Радиус – вектор, характеризующий положение частицы  относительно неподвижной точки
относительно неподвижной точки  , меняется со временем по закону
, меняется со временем по закону  ,
,  ,
,  . Найти ускорение
. Найти ускорение  частицы и уравнение ее траектории
частицы и уравнение ее траектории  , взяв оси
, взяв оси  и
и  совпадающими по направлению с векторами
совпадающими по направлению с векторами  и
и  .
.
Решение
Продифференцировав  по времени дважды, получим ускорение:
по времени дважды, получим ускорение:
 ,
,
т.е. вектор  все время направлен к точке
все время направлен к точке  - начало координат, а его модуль пропорционален
- начало координат, а его модуль пропорционален  .
.
Теперь найдем уравнение траектории. Проекции вектора  на оси
на оси  и
и  имеют вид:
имеют вид:
 ,
,  .
.
Исключим  из этих двух уравнений:
из этих двух уравнений:
 ,
, 
учитывая, что  , получим
, получим

Это уравнение эллипса,  и
и  – его полуоси (рис.1.9). Частица движется по часовой стрелке.
– его полуоси (рис.1.9). Частица движется по часовой стрелке.
Рис.1.9
Задача 5Тангенциальное и нормальное ускорения
Точка движется замедленно по окружности радиуса  так, что ее тангенциальное и нормальное ускорения в каждый момент равны друг другу по модулю. В начальный момент точке была сообщена скорость
так, что ее тангенциальное и нормальное ускорения в каждый момент равны друг другу по модулю. В начальный момент точке была сообщена скорость  . Найти скорость
. Найти скорость  и модуль полного ускорения
и модуль полного ускорения  точки в зависимости от пройденного пути
точки в зависимости от пройденного пути  .
.
Решение
По условию  ,
,  , будем иметь
, будем иметь  ;
;  .
.
Подставив  , преобразуем исходное уравнение к виду:
, преобразуем исходное уравнение к виду:

Проинтегрируем это уравнение с учетом начальной скорости:
 .
.
Получим  или
или  .
.
В данном случае  , поэтому модуль полного ускорения
, поэтому модуль полного ускорения  или
или  .
.
Задача 6 Материальная точка начинает двигаться по окружности радиуса  = 10 см с постоянным тангенциальным ускорением
= 10 см с постоянным тангенциальным ускорением  = 0,4 см/с2. Через какой промежуток времени вектор ускорения
= 0,4 см/с2. Через какой промежуток времени вектор ускорения  образует с вектором скорости
образует с вектором скорости  угол
угол  , равный 600 и 800? Какой путь пройдет за это время движущаяся точка? На какой угол повернется радиус – вектор
, равный 600 и 800? Какой путь пройдет за это время движущаяся точка? На какой угол повернется радиус – вектор  , если в начальный момент времени он направлен вертикально вверх?
, если в начальный момент времени он направлен вертикально вверх?
Решение
Рис. 1.10
Из рис.1.10 видно, что
 . (1)
. (1)
Тангенциальное ускорение

Следовательно, линейная скорость движущейся точки (при  ):
):  .
.
Нормальное ускорение  .
.
Подставляя в формулу (1), находим

Тогда время и путь соответственно равны:
 , (2)
, (2)
 . (3)
. (3)
Угол поворота  изменяется со временем также по квадратичному закону
изменяется со временем также по квадратичному закону
 (4)
(4)
При ε1= 600 (  ), согласно выражениям (2) – (4),
), согласно выражениям (2) – (4),  = 6,6 с,
= 6,6 с,  = 8,7 см,
= 8,7 см,  = 0,87 рад.
= 0,87 рад.
При ε2= 600 (  ),
),  = 12 с,
= 12 с,  = 28 м,
= 28 м,  = 2,8 рад
= 2,8 рад
Задача 7Вращение твердого тела Твердое тело вращается вокруг неподвижной оси по закону  , где
, где  и
и  - некоторые положительные постоянные. Найти характер движения этого тела.
- некоторые положительные постоянные. Найти характер движения этого тела.
Решение
Угловая скорость  , отсюда
, отсюда  .
.
Угловое ускорение  .
.
Отсюда видно, что тело, вращаясь равнозамедленно (  ), останавливается в момент
), останавливается в момент  , а затем направление вращения (знак
, а затем направление вращения (знак  ) изменяется на противоположное.
) изменяется на противоположное.
Тесты
1. При вращательном движении линейную скорость в СИ измеряют в…(
1) …в метрах в секунду в квадрате [м/с2]; 2) …в метрах в секунду [м/с]; 3) радианах в секунду в квадрате [рад/с2]; 4) …в градусах в секунду [º/с]; 5) …радианах в секунду [рад/с].
2. Пусть ω0 – угловая скорость в момент времени t = 0, ε – угловое ускорение, тогда угловая скорость при равнозамедленном вращении в момент времени t равна…
1) …  ; 2) …
; 2) …  ; 3) …
; 3) …  ; 4) …
; 4) …  ; 5) …
; 5) …  .
.
3. Тело вращается по орбите с частотой 10 с-1. Найти угловую скорость вращения тела, если тангенциальная составляющая скорости 2 м/с.
1) …62,8 рад/сек; 2) …0,2 рад/сек; 3) …6,28 рад/сек; 4) …20 рад/сек.
4. Тело движется прямолинейно вдоль оси  . Зависимость проекции скорости тела на ось
. Зависимость проекции скорости тела на ось  от времени представлена на рисунке 1.11. Путь, пройденный телом за первые 12 с равен…
от времени представлена на рисунке 1.11. Путь, пройденный телом за первые 12 с равен…
1) …67.5 м; 2) …12.5 м; 3) …15 м;4) …80 м; 5) …65 м.

Рис. 1.11
5. Точка А движется по спирали с постоянной по величине скоростью (рис.1.12), при этом величина нормального ускорения уменьшается. В каком направлении движется точка?
1) …1; 2) …2; 3) …3; 4) …4; 5) …5.
Рис. 1.12
6. При вращательном движении угловое ускорение в СИ измеряют в…
1) …в метрах в секунду в квадрате [м/с2]; 2) …в метрах в секунду [м/с]; 3) …радианах в секунду в квадрате [рад/с2]; 4) …в градусах в секунду [º/с]; 5) …радианах в секунду [рад/с].
7. Пусть ω0 – угловая скорость в момент времени t = 0, ε – угловое ускорение, тогда угловая скорость при равномерном вращении в момент времени t равна…
1) …  ; 2) …
; 2) …  ; 3) …
; 3) …  ; 4) …
; 4) …  ; 5) …
; 5) …  .
.
8. Тело движется по окружности радиусом 0,1 м и за время 0,1 с совершает 10 полных оборотов. Угловая скорость вращения тела равна…
1) …0,628 рад/сек; 2) …6,28 рад/сек; 3) …628 рад/сек; 4) …62,8 рад/сек.
9. Тело движется прямолинейно вдоль оси  . Зависимость проекции скорости тела на ось
. Зависимость проекции скорости тела на ось  от времени представлена на рисунке 1.11. Путь, пройденный телом за первые 15 с равен…
от времени представлена на рисунке 1.11. Путь, пройденный телом за первые 15 с равен…
1) …77.5 м; 2) …55 м; 3) …37.5 м; 4) …– 80 м; 5) 70 м.
10. При вращательном движении тангенциальное ускорение в СИ измеряют в…
1) …в метрах в секунду в квадрате [м/с2]; 2) …в метрах в секунду [м/с]; 3) …радианах в секунду в квадрате [рад/с2]; 4) …в градусах в секунду [º/с]; 5) …радианах в секунду [рад/с].
11. Пусть ω0 – угловая скорость в момент времени t = 0, ε – угловое ускорение, тогда угол поворота за время t при равноускоренном вращении равен…
1) …  ; 2) …
; 2) …  ; 3) …
; 3) …  ; 4) …
; 4) …  ; 5) …
; 5) …  .
.
12. Тело движется по окружности диаметром 20 см и за время 10 с оно совершает 100 полных оборотов. Период вращения этого тела равен…
1) …0,1 с; 2) …1 с; 3) …0,01 с; 4) …10 с; 5) …100 с.
13. Тело движется прямолинейно вдоль оси  . Зависимость проекции скорости тела на ось
. Зависимость проекции скорости тела на ось  от времени представлена на рисунке 11. Модуль перемещения тела за первые 3 с равен…
от времени представлена на рисунке 11. Модуль перемещения тела за первые 3 с равен…
1) …37.5 м; 2) …22.5 м; 3) …15 м; 4) …7.5 м; 5) …– 22.5 м.
14. Куда направлено тангенциальное ускорение при равномерном вращении точки по окружности (рис.1.13)….
Рис. 1.13
1) …1; 2) …2; 3) …3; 4) …4; 5) …равно нулю.
15. Вращающийся диск сделал за 20 с 50 оборотов. Определите частоту его вращения…
1) …0,4 Гц; 2) …400 Гц; 3) …2,5 Гц; 4) …4 Гц; 5) …1000 Гц.
16. Тело движется прямолинейно вдоль оси  . Зависимость проекции скорости тела на ось
. Зависимость проекции скорости тела на ось  от времени представлена на рисунке 1.11. Модуль перемещения тела за первые 9 с равен
от времени представлена на рисунке 1.11. Модуль перемещения тела за первые 9 с равен
1) …40 м; 2) …46 м; 3) …80 м; 4) …50 м; 5) …– 50 м.
17. Три спутника вращаются равномерно вокруг некоторой планеты, по орбитам, показанным на рисунке 1.14. В каком из нижеприведенных соотношений между собой находятся их скорости?
Рис. 1.14
1) … V 1 = V 2 > V 3 ; 2) … V 1 = V 2 < V 3 ; 3) … V 2 = V 2 = V 3 ; 4) … V 3 > V 2 > V 1 ; 5) …V3 < V 2 < V 1.
18. В СИ основной единицей измерения частоты является…
1) …герц [с-1]; 2) …радиан в секунду [рад/с]; 3) …секунда [с]; 4) …радиан [рад]; 5) …сантиметр [см].
19. Три спутника вращаются равномерно вокруг некоторой планеты, по орбитам показанным на рисунке 1.14. В каком из нижеприведенных соотношений между собой находятся периоды их обращения?
1) …Т1 = Т2 > Т3; 2) …Т1 = Т2 < Т3; 3) …Т2 = Т1 = Т3; 4) …Т3 > Т2 > Т1; 5) …Т3 < Т2 < Т1.
20. Тело движется прямолинейно вдоль оси  . Зависимость проекции скорости тела на ось
. Зависимость проекции скорости тела на ось  от времени представлена на рисунке 1.11. Модуль перемещения тела за первые 15 с равен
от времени представлена на рисунке 1.11. Модуль перемещения тела за первые 15 с равен
1) …77.5 м; 2) …5 м; 3) …37.5 м; 4) …– 5 м; 5) …70 м.
Дата добавления: 2021-03-18; просмотров: 91; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
