Нелінійні операції над векторами.

Скалярний добуток.

Скалярним добутком двох векторів  і  називається число, яке дорівнює добутку їхніх модулів на косинус кута між ними. Скалярний добуток векторів  і  позначається символом . Якщо позначити кут між вектором  і  через φ, для скалярного добутку будемо мати вираз

.

Властивості скалярного добутку:

1. =  -  комутативна (переставна) властивість;

2.  - асоціативна (сполучна) властивість відносно множення на число;

3.  - дистрибутивна (розподільна) властивість.

З визначення скалярного добутку випливає, що косинус кута між двома ненульовими векторами  і   дорівнює . Звідси робимо висновок, що два вектора  і   перпендикулярні (φ = ) тоді і тільки тоді, коли = 0.

Якщо вектори  і  задані своїми координатами (а_х, а_у, а_z) i (b_x, b_y, b_z) відповідно, то ці вектори мають вигляд

,    .

Їхній скалярний добуток обчислюється за формулою

,

а косинус кута φ між цими векторами дорівнює

.

Звичайно, якщо вектори  і  перпендикулярні між собою, то

.

    Приклад. Вектори 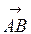і  задані своїми координатами 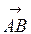(2, -1, 2),  (3, 0, 4). Знайти скалярний добуток цих векторів і кут між ними.

    Розв’язання:  

    =2 ∙3 – 1 ∙0 + 2 ∙4 = 14;

     .

    Відповідь: =14;  .

 Векторний добуток.

Векторним добутком векторів  і   називається вектор , який визначається такими умовами:

1) його модуль дорівнює ,  де φ – кут між векторами  і ;

2) вектор  перпендикулярний кожному з векторів  і ;

3) вектор спрямований таким чином, щоб найкоротший оберт від  до  навколо вектора  відбувався проти годинникової стрілки, якщо дивитися з кінця вектора .

 

 

Векторний добуток векторів  і  позначаються символом .

Якщо вектори  і  колінеарні, то φ = 0 і , отже, векторний добуток відносно таких векторів дорівнює нулю:  = 0.

Властивості векторного добутку

1. =-  -  не має переставної властивості,

2.  -  сполучна властивість відносно множення на число;

3. =-  - розподільна властивість.

Векторний добуток    = 0, якщо вектори  і   колінеарні або будь-який з векторів є нульовим.

Якщо вектори  і задані своїми координатами:  (а_х, а_у, а_z),  (b_x, b_y, b_z),

то векторний добуток можна записати за допомогою детермінанта

 

              .

Приклад. . Вектори 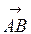і  задані своїми координатами 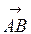( - 2, 2 , 1 ),  ( 4 , 3 , 0 ). Знайти модуль векторного добутку цих векторів.

Розв’язання: ;

                 ;

                  ;

                 ;

                 ;

                  .

 Відповідь: .

 

---

Дата добавления: 2020-12-12; просмотров: 49; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!