Дисперсия дискретной случайной величины.
Лекция 2
Математическое ожидание и дисперсия дискретной случайной величины
Математическое ожидание дискретной случайной величины
При решении многих практических задач нет необходимости характеризовать случайную величину полностью (законом распределения), а достаточно в сжатой форме выразить наиболее существенные особенности.
О каждой случайной величине необходимо прежде всего знать ее некоторое среднее значение, а также какое-либо число, характеризующее степень разбросанности ее возможных значений относительно среднего. Это так называемые числовые характеристики случайной величины – математическое ожидание и дисперсия.
Рассмотрим сначала дискретную случайную величину  , которая принимает возможные значения
, которая принимает возможные значения  ,
, 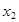 , ..,
, ..,  с вероятностями
с вероятностями 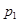 ,
,  , ..,
, ..,  . Тогда математическое ожидание случайной величины
. Тогда математическое ожидание случайной величины  , которое мы обозначим
, которое мы обозначим  , определяется равенством
, определяется равенством
 .
.
Если дискретная случайная величина  может принимать бесконечное счетное множество значений
может принимать бесконечное счетное множество значений  ,
, 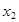 , ..,
, ..,  , … с вероятностями
, … с вероятностями 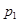 ,
,  , ..,
, ..,  , …, то ее математическое ожидание определяется равенством
, …, то ее математическое ожидание определяется равенством
 .
.
Математическим ожиданием дискретной случайной величины  называется сумма произведений всех возможных ее значений на соответствующие вероятности.
называется сумма произведений всех возможных ее значений на соответствующие вероятности.
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Происхождение термина “математическое ожидание” связано с начальным периодом возникновения теории вероятности (XVI-XVII в.в.), когда область ее применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша, или иными словами – математическое ожидание выигрыша.
|
|
|
Пример 7. Дан закон распределения вероятностей дискретной случайной величины  :
:

| -3 | -1 | 1 | 2 |

| 0,1 | 0,2 | 
| 0,3 |
Найти вероятность  и математическое ожидание этой случайной величины.
и математическое ожидание этой случайной величины.
Решение. Вероятность  найдем из условия
найдем из условия  , тогда
, тогда  .
.
По определение математическое ожидание дискретной случайной величины равно
 .
.
Свойства математического ожидания
Свойство 1. Математическое ожидание постоянной величины равно самой постоянной.
 .
.
Доказательство. Будем рассматривать постоянную  как дискретную случайную величину, которая имеет одно возможное значение
как дискретную случайную величину, которая имеет одно возможное значение  и принимает его с вероятностью
и принимает его с вероятностью  . Следовательно,
. Следовательно,  .
.
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
 .
.
Доказательство. Если случайная величина  задана законом распределения
задана законом распределения

| 
| 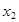
| … | 
|

| 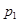
| 
| … | 
|
то в силу первого действия над дискретными случайными величинами закон распределения для  будет иметь вид:
будет иметь вид:
|
|
|

| 
| 
| … | 
|

| 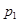
| 
| … | 
|
Тогда
 .
.
Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме математических ожидание слагаемых:
 .
.
Доказательство. Чтобы упростить вывод, мы ограничимся лишь двумя возможными значениями каждой из величин.

| 
| 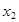
| 
| 
| 
| |||

| 
| 
| 
| 
| 
|
Составим закон распределения вероятностей дискретной случайной величины для суммы  в силу второго действия над дискретными случайными величинами:
в силу второго действия над дискретными случайными величинами:

| 
| 
| 
| 
|

| 
| 
| 
| 
|
Математическое ожидание равно сумме произведений всех возможных значений на их вероятности, т.е.

 .
.
Сумма вероятностей в скобках равна единице, поэтому окончательно получим:
 .
.
Свойство 4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
 .
.
Доказательство аналогичное предыдущему.
Пример 8. Две независимые случайные величины заданы законами распределения:

| -2 | 0 | 1 | 3 | 
| -5 | 1 | 4 | |||

| 0,3 | 0,2 | 0,4 | 0,1 | 
| 0,1 | 0,6 | 0,3 |
Вычислить: 1)  ; 2)
; 2)  .
.
Решение.
1) Вычислим сначала математическое ожидание дискретной случайной величины  .
.
|
|
|
 .
.
Теперь воспользуемся первыми тремя свойствами математического ожидания:
 .
.
2) Найдем предварительно математическое ожидание дискретной случайной величины (5.8)  .
.
 .
.
По 4 свойству математического ожидания:
 .
.
Дисперсия дискретной случайной величины.
Дата добавления: 2020-11-27; просмотров: 58; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
