VI.Выполнение теста по вариантам
Конспект урока математики
Дата
| 95 | 96 | 97 | 98 |
| 29.10.20 |
Группа № 95 профессия мастер по ремонту и обслуживанию автомобилей курс 1
Группа №96 профессия повар, кондитер курс1
Группа №97 профессия машинист крана(крановщик) курс 1
Группа №98 профессия тракторист-машинист сельскохозяйственного производства
Курс 1
Тема урока Показательные уравнения »
Урок №27
Форма работы: индивидуальная, дистанционное обучение.
Тип урока: урок изучения нового материала.
Цель урока: формировать систему знаний и умений, связанных с решением показательных уравнений
Ключевые слова: показательные уравнения .
Изучаемая литература: Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.
10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г
Интернет- ресурсы : Математика в открытом колледже http://www.mathematics.ru
Ход занятия :
Организационный этап. Мотивационный модуль
Ребята, сегодня, вы познакомитесь с темой « Показательные уравнения, рассмотрите примеры решения показательных уравнений Научившись решать такие уравнения, вы смело будете решать показательные неравенства Показательные уравнения широко используются при решении химических и физических задач.
Основная часть. Объясняющий модуль.
План изучения:
· простейшие показательные уравнения;
· Способы решения показательных уравнений
· графический метод решения показательных уравнений;
Показательным называется уравнение, в котором переменная входит только в показатели степеней, при заданном основании.
Уравнения вида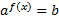 
, 
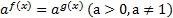называются простейшими показательными уравнениями.
Вспомним, что показательная функция при a>1 монотонно возрастает и принимает все положительные значения, каждое ровно один раз. В случае 0<a<1 показательная функция монотонно убывает и также принимает все положительные значения, каждое ровно один раз.
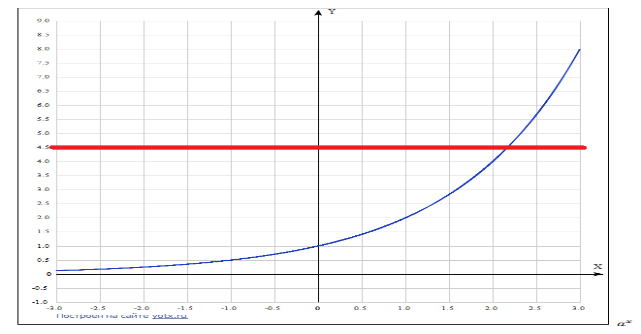
Рисунок 1 – иллюстрация решения простейшего показательного уравнения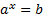 
, a>1.
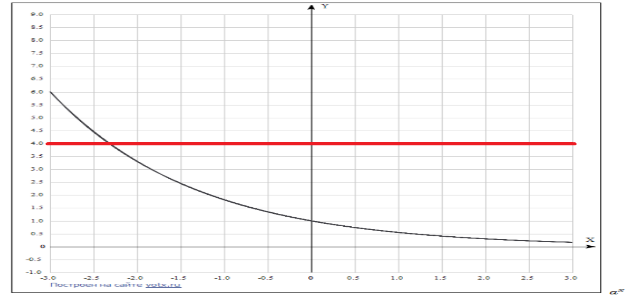
Рисунок 2 – иллюстрация решения простейшего показательного уравнения 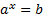, 0<a<1.
Способы решения показательных уравнений
Приведение обеих частей уравнений к одному и тому же основанию.
Замена переменной.
Вынесение общего множителя за скобки.
Закрепление темы . Тренировочный модуль. Рассмотрите задания, решаемые разными способами
Метод уравнивания оснований.
Примеры.
Пример 1. Решите уравнение: 27 
- 
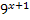= 0 .
Решение.
27 - 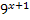= 0 <=> 33 
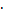34x-9- (32)x+1 = 0 <=> 33+ (4x-9)- 32(x+1) = 0<=> 34x-6-32x+2 = 0 <=> 34x-6 = 32x+2<=> 4x-6=2x+2 <=> 2x = 8 <=> x=4.
Ответ: 4.
Уравнения, решаемые разложением на множители.
Пример 2 . Решите уравнение: x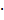 
2x = 2 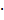2x + 8x-16.
Решение.
x 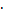2x = 2 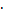2x + 8x-16 <=> x 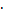2x - 2 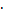2x = 8 
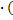x-2) <=> 2x 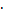(x-2) - 8 
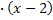<=> (x-2) 
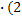x - 8) = 0 <=> 
<=> 
<=> 
<=> 
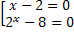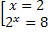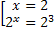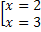
Ответ: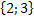 
Замена переменной
Пример 1 . Решите уравнение: 22+x - 22-x = 5.
Решение.
22+x - 22-x = 5 <=> 22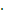 
2x -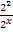 
= 15 <=> 4 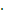(2x)2 - 4 = 15 
x
Делаем замену t = 2 x , t > 0. Получаем уравнение 4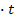 
2 - 4 = 15t <=> 4t 2 - 15t - 4=0
<=> 
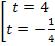, t = 
не удовлетворяет условию t > 0.
Вернемся к переменной х:
2х = 4<=> 2x = 22 <=> x=2.
Домашнее задание : 1. составить конспект по теме урока
2.Контрольное задание:
VI.Выполнение теста по вариантам
1 вариант
1.Найдите корень уравнения: 27х = -27
а) нет корней б) – 1 в) 0
2.Найдите корень уравнения: 9 -9+х=729
а) -6 б) 12 в) -12
3. Найдите корень уравнения: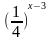 
= 64
а) 6 б) 9 в) 0
4. Найти сумму корней уравнения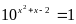 
а) 1 б) -1 в) 9
5. Укажите промежуток, которому принадлежит корень уравнения
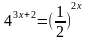
а)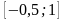 
б) (5; 7) в)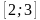 
2 вариант
1.Найдите корень уравнения: 125х = -125
а) нет корней б) 3 в) 5
2.Найдите корень уравнения: 5 3 - х=125
а) -3 б) 0 в) -1
3. Найдите корень уравнения: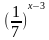 
= 49
а) - 3 б) 5 в) 1
4. Найдите сумму корней уравнения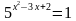 
а) – 2 б) 3 в) - 3
5. Укажите промежуток, которому принадлежит корень уравнения
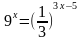
а)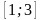 
б) (0; 1) в)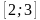
Дата добавления: 2020-11-23; просмотров: 43; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!