Отправить личным сообщением в ВК
Конспект урока математики
Дата
| 95 | 96 | 97 | 98 |
| 5.11.20; 7.11.20 |
Группа № 95 профессия мастер по ремонту и обслуживанию автомобилей курс 1
Группа №96 профессия повар, кондитер курс1
Группа №97 профессия машинист крана(крановщик) курс 1
Группа №98 профессия тракторист-машинист сельскохозяйственного производства
Курс 1
Тема урока: «Системы показательных уравнений и неравенств»
Урок №31-32
Форма работы: индивидуальная, дистанционное обучение.
Тип урока: урок изучения нового материала.
Цель урока: формировать систему знаний и умений, связанных с решением систем показательных уравнений и неравенств.
Ключевые слова: показательные уравнения и системы показательных уравнений, однородные уравнения, системы показательных неравенств.
Изучаемая литература: Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.
10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г
Интернет- ресурсы : Математика в открытом колледже http://www.mathematics.ru
Ход занятия :
Организационный этап. Мотивационный модуль
Ребята, сегодня, вы познакомитесь с темой « Системы показательных уравнений и неравенств »,рассмотрите примеры решения по теме.
Основная часть. Объясняющий модуль.
План изучения:
1. Повторение понятий показательные уравнения и неравенства.
2.системы показательных уравнений и их решение.
3.системы показательных неравенств и способы их решения.
Показательным называется уравнение, в котором переменная входит только в показатели степеней, при заданном основании.
Уравнения вида 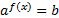 ,
, 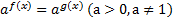 называются простейшими показательными уравнениями.
называются простейшими показательными уравнениями.
Так как множество значений показательной функции 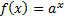 - множество положительных чисел, то при
- множество положительных чисел, то при 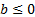 уравнение решений не имеет.
уравнение решений не имеет.
Теперь рассмотрим случай b>0.
Вспомним, что показательная функция при a>1 монотонно возрастает и принимает все положительные значения, каждое ровно один раз. В случае 0<a<1 показательная функция монотонно убывает и также принимает все положительные значения, каждое ровно один раз.
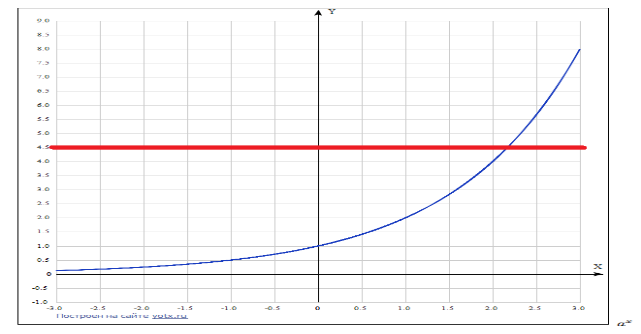
Рисунок 1 – иллюстрация решения простейшего показательного уравнения  , a>1.
, a>1.
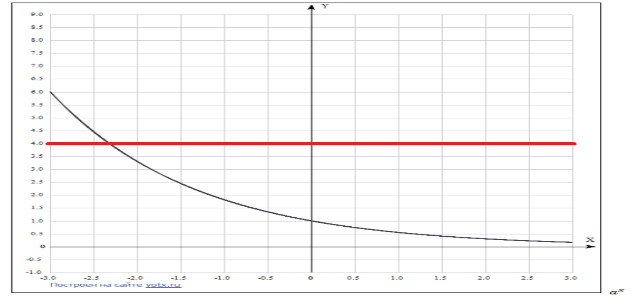
Рисунок 2 – иллюстрация решения простейшего показательного уравнения  , 0<a<1.
, 0<a<1.
Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.
Cистемы неравенств, состоящие из показательных неравенств, называются системой показательных неравенств.
1. При решении систем показательных уравнений и неравенств, применяются те же приемы, что при решении систем алгебраических уравнений и неравенств
1.метод подстановки,
2.метод сложения,
3.метод введения новых переменных.
Во многих случаях, прежде чем применить тот или иной метод решения, следует преобразовать каждое уравнение (неравенство) системы к возможно более простому виду.
Закрепление . Тренировочный модуль
№1 Решение системы: 
Введем новые переменные:  .
.
Рассмотрим вспомогательную систему:
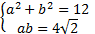 .
.
Возведем второе уравнение в квадрат:
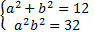 . Решим полученную систему относительно
. Решим полученную систему относительно 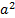 и
и  .
.
 или
или 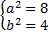 .
.
Так как 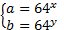 , то есть положительные, то
, то есть положительные, то
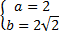 или
или 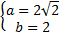 .
.
Вернемся к исходным переменным.
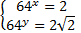 или
или  .
.
Отсюда:
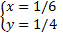 или
или 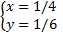 .
.
Ответ: (1/6; 1/4); (1/4; 1/6)
№2 Рассмотрите решение неравенства

т.к. функция у=3t возрастает,
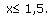
№3. Решение системы неравенств.
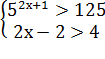
Решение; 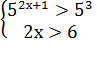
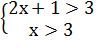
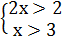
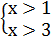
Постройте числовой луч, отметьте на нем решение, запишите ответ
Домашнее задание 1. составить конспект по теме урока
2.Выполнить контрольные задания :
Пример 1:Решите систему уравнений
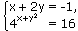
Задание 2. Решите систему неравенств 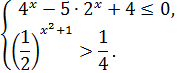
отправить личным сообщением в ВК
Дата добавления: 2020-11-23; просмотров: 52; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
