Правильная пирамида, определение, свойства, задача

Занятие по математике №33 Группа 2ВГ Дата проведения:10.11.20г.

Тема: Решение задач

Выполненные задания отправлять на электронную почту: tatiefremenko@yandex.ua

или страницу вКОНТАКТЕ - https://vk.com/id592773352

Индивидуальные консультации, оценивание устных ответов по тел.:

0660627421, 0721813966 Ефременко Т.А.

Домашнее задание: повторить §1,2 ,стр.60,69, «Геометрия 10-11 класс» Атанасян, составить краткий конспект занятия, рассмотреть и записать в тетрадь примеры решения задач.

Видеофильм просмотреть по ссылке: https://yandex.fr/video/preview?filmId=4472411058602919366&parent-reqid=1604606182518354-224829241943481511600107-production-app-host-man-web-yp-137&path=wizard&text=Решение+задач+Многоугольники+геометрия+10+класс&wiz_type=vital

Учебный материал для самостоятельного изучения

На данном занятии мы решим несколько задач по теме «Многогранники», наибольшее внимание уделим пирамиде и призме, как самым распространенным видам многогранника.

Правильная призма и прямой параллелепипед, определение, свойства

Правильная треугольная призма:

Рис. 1. Правильная треугольная призма

-данная призма прямая – боковое ребро перпендикулярно плоскостям оснований;

-в основаниях лежат правильные треугольники.

Задача о вершинах и ребрах призмы

Задача 1

Укажите число плоскостей симметрии у правильной треугольной призмы.

Ответ: 4

Решение:

Пусть и М – середины ребер и АВ соответственно (рисунок 1). Вершине соответствует плоскость симметрии . данная плоскость является плоскостью симметрии потому что ребро АВ перпендикулярно МС по свойствам правильного треугольника и перпендикулярно по свойствам прямой призмы. Значит ребро АВ перпендикулярно плоскости . аналогично ребро перпендикулярно той же плоскости. Так, при выполнении симметрии точка А перейдет в точку В и наоборот; точка перейдет в точку и наоборот; точки и С останутся без изменений. То есть призма переходит сама в себя.

Мы рассмотрели плоскость симметрии относительно вершины , таких вершин три – значит три плоскости симметрии. Четвертая плоскость симметрии проходит через середины боковых ребер (рисунок 2).

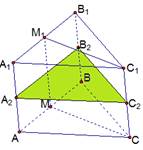
Рис. 2. Плоскость симметрии правильной треугольной призмы

Других плоскостей симметрии рассматриваемая призма не имеет, т. к. наличие плоскостей симметрии связано с количеством осей симметрии в основаниях и боковых гранях фигуры.

Прямоугольный параллелепипед:

Определение.

Прямоугольный параллелепипед – это такой прямой параллелепипед, у которого в основании лежит прямоугольник. Рис. 3.

Рис. 3. Прямоугольный параллелепипед

-все грани прямоугольного параллелепипеда являются прямоугольниками;

-все диагонали равны между собой: ;

-квадрат диагонали равен сумме квадратов всех измерений: ;

-точка О пересечения диагоналей делит их пополам.

Задача 2

Докажите, что число вершин любой призмы четно, а число ребер кратно трем.

Решение: пусть задана n-угольная призма. Количество вершин призмы равно удвоенному количеству вершин основания, то есть 2n, а такое число кратно двум при любом n – мы доказали, что число вершин любой призмы четно.

Число ребер призмы состоит из ребер оснований и боковых ребер. Основания содержат 2n ребер и еще n ребер – боковые ребра. Всего призма содержит 3n ребер, что кратно трем при любом n – мы доказали, что число ребер любой призмы кратно трем.

Задачи на куб

Напомним, что куб – это частный случай прямоугольного параллелепипеда, все его грани – это квадраты.

Задача 3

d – диагональ куба. Найти площадь полной поверхности куба.

Решение:

Рис. 4. Иллюстрация к задаче 3

Пусть ребро куба равно , тогда по свойству прямоугольного параллелепипеда:

– это площадь одной грани, куб состоит из шести одинаковых граней, имеем площадь полной поверхности:

Задача 4

В кубе найти угол между скрещивающимися прямыми и BD.

Решение:

Рис. 5. Иллюстрация к задаче 4

Проведем прямую , она параллельна прямой BD. Значит искомый угол – это угол . Он равен , так как треугольник равносторонний – его стороны равны как диагонали равных квадратов.

Правильная пирамида, определение, свойства, задача

Определение.

Рис. 6. Правильная четырехугольная пирамида

Правильной называется пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр этого многоугольника (рисунок 6).

Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на апофему:

Определение.

Апофемой называется высота боковой грани пирамиды.

Задача 5

В правильной четырехугольной пирамиде ребро основания и высота равны 2. Найти расстояние от центра основания до боковой грани.

Решение:

Рис. 7. Иллюстрация к задаче 5

Пусть задана пирамида с основанием ABCD и вершиной S. Из условия ABCD – квадрат, пусть О – точка пересечения его диагоналей, тогда SO – высота пирамиды. . Требуется найти расстояния от точки О до плоскости CSD. Расстоянием от точки до плоскости называется длина перпендикуляра опущенного из заданной точки на плоскость.

Пусть точка М – середина DС. Опустим перпендикуляр ОК на апофему SM. Докажем, что построенный таким образом отрезок ОК перпендикулярен всей плоскости CSD. Поскольку CD перпендикулярно всей плоскости MOS, то ОK⊥CD. Так, ОК есть перпендикуляр к плоскости CDS, его и требуется найти.

Рассмотрим прямоугольный треугольник MOS. В нем как средняя линия треугольника DBC. Имеем . SO по условию равно 2. Найдем гипотенузу MS по теореме Пифагора: .

Найдем площадь рассматриваемого треугольника двумя способами:

Задача на прямую призму

Задача 6

Боковое ребро прямой призмы равно единице. . , М – середина . Найти .

Решение:

Для наглядности произведем сечение призмы заданной плоскостью ВСМ. Для этого проведем MN параллельно , полученная фигура и будет искомым сечением (рисунок 8).

Рис. 8. Иллюстрация к задаче 7

Чтобы найти расстояние от точки до плоскости ВСМ, нужно опустить из этой точки перпендикуляр к плоскости. Опустим перпендикуляр к прямой СМ и докажем, что он является перпендикуляром ко всей плоскости ВСМ.

Из условия: ; , отсюда ., т. к. .

Так, перпендикулярно двум прямым из плоскости сечения ВСМ: ВС и СМ, эти прямые пересекаются, отсюда перпендикулярно всей плоскости сечения, значит – искомое расстояние от точки до плоскости.

Рассмотрим прямоугольный треугольник . в нем по условию, . Найдем гипотенузу СМ по теореме Пифагора:

Запишем площадь треугольника двумя способами:

Подведение итогов занятия. Итак, мы рассмотрели наиболее распространенные задачи на многогранники, уделили внимание пирамиде, призме, прямоугольному параллелепипеду. Также мы вспомнили свойства основных многогранников.

Дата добавления: 2020-11-23; просмотров: 102; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!