Полный резерв времени для задач критической работы, в отличие от критического пути, может быть отличен от нуля.
Так, положим, длительности всех обменов в системе работ, граф которой показан на рис. 1, одинаковы и равны одной единице времени. Критической является работа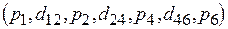 
, ее априорная максиминная длительность равна 12 единицам времени (см. табл. 1). После назначения задач этой работы очередной критической является работа 
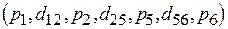: не распределены ресурсы между задачами 
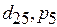и 
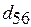, а длительность работы составляет 11 единиц. Пут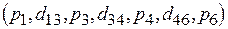и 
и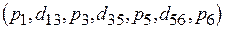 
представляют критические работы, априорная оценка длительности выполнения которых равна соответственно 10 и 9 единицам времени.
Свойство аддитивной сепарабельности критерия (2.4) позволяет свести проблему распределения ресурсов для заданной системы задач к последовательному распределению ресурсов между задачами различных критических работ.
Разрешение коллизийнеобходимо осуществлять так, чтобысохранялся промежуточный план выполнения задач и не ухудшались показатели загрузки ресурсов (2.7): по крайней мере, не должны уменьшаться коэффициенты загрузки базовых процессоров и не должна увеличиваться загрузка коммуникационной подсистемы. Первое из условий служит естественным сдерживающим фактором при введении дополнительных процессоров в состав ресурсов вычислительной системы.
Сохранение промежуточного плана, с одной стороны, обеспечивает сходимость алгоритмов планирования, а с другой, обуславливает «недоиспользование» процессами вычислений возможного времени их выполнения и, соответственно, погрешность планирования.
|
|
|
В основу распределения ресурсов в пределах одной критической работы может быть положена модификация схемы, основанной на аппарате динамического программирования.
Суть подхода заключается в следующем.
Пусть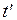 
– крайний срок завершения работы 
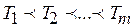. Для каждой из переменных 
, 
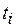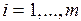, соответствующей времени выполнения задачи 
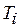, зададим диапазон ее изменения:
, 
, 
,
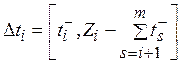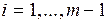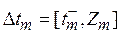где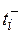 
, 
, 
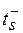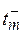– нижние границы диапазонов, а 
, 
, 
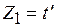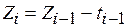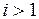, представляют запасы по времени к моменту начала решения задач 
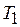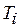, . Шаг изменения , 
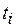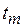в диапазонах 
, 
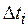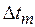не меньше 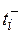, , 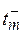которые, в свою очередь, определяются производительностью используемого процессора или характеристиками коммуникационной среды. Частная функция 
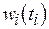в критерии 
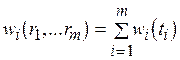(см. (2.4)) определена на отрезках 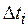, верхние границы которых зависят от значения соответствующего запаса 
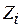, и, следовательно, может быть представлена как функция 
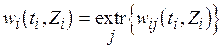, где 
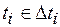, а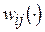 
– частная функция для соответствующего типа ресурса (см., например, (2.5), (2.6)).
Рассмотрим процедуру так называемой обратной прогонки от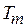 
к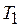 
. Для всех задач, кроме первой 
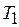, отыскивается условно оптимальная длительность выполнения, при которой 
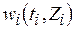достигает условного оптимума 
.
|
|
|
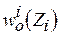Обратная прогонка осуществляется в соответствии со следующим функциональным уравнением
(3.1)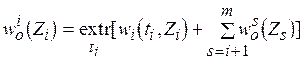 
,
, 
, 
.
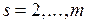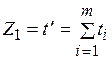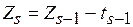Пусть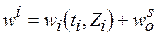 
, где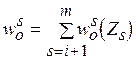 
.
Процедура так называемой прямой раскрутки от 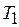к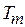 
позволяет определить оптимальные длительности выполнения задач в соответствии со следующим рекуррентным соотношением:
(3.2)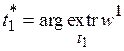 
, 
,
, 
, 
,
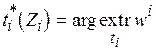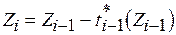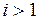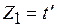где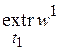 
, 
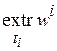получаются из уравнения (3.1).
Для набора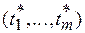 
из (3.2) определяются моменты 
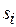запуска задач и назначения на ресурс
(3.3)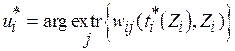 
.
Критическая работа может содержать и отдельные не назначенные задачи, что определяется конкретным видом информационно-логического графа задания и крайними сроками (2.3) завершения задач, входящих в систему работ. Для отдельной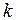 
-й задачи диапазон изменения длительности ее выполнения зависит от запаса 
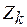по времени: 
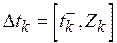. Запас, в свою очередь, может зависеть от крайнего срока завершения выполнения задачи. Оптимальные длительность и назначение для задачи 
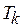отыскиваются в соответствии со следующими функциональными уравнениями:
(3.4)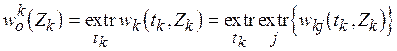 
,
(3.5)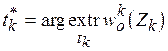 
,
(3.6)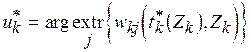 
.
Выражения (3.4) - (3.6) являются частными случаями уравнений (3.1) - (3.3).
Таким образом, распределение ресурсов для системы задач может быть осуществлено на основе применения уравнений (3.1) - (3.6) к последовательности критических работ и разрешения коллизий между задачами обработки, конкурирующими за один и тот же процессор.
|
|
|
Теорема 1. Пусть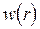 
– аддитивно-сепарабельный критерий эффективности (2.4) распределения ресурсов (2.1), осуществляемого на основе функциональных уравнений (3.1) - (3.6), для последовательности 
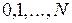ранжированных критических работ, состоящих, в свою очередь, из 
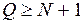из работ и отдельных задач. Коллизии разрешаются за счет дополнительных процессоров, тип которых совпадает с соответствующим типом базового. Оптимальная длительность выполнения критических работ 
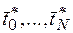определяется оптимальной длительностью работ и задач 
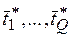, причем 
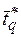, где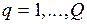 
, является отрезком одной и только одной последовательности 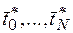, где 
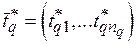, а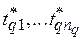 
– оптимальные значения длительности для каждой из 
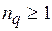задач.
При этом
(3.7)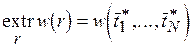 
.
Доказательство теоремы 1 приводится в Приложении.
Нужно подчеркнуть, что (3.7) справедливо тогда, когда при разрешении коллизий не изменяется достигнутый промежуточный план выполнения задач и вводится процессор того же типа, что и базовый, за который конкурируют задачи.
|
|
|
Если же коллизии разрешаются за счет использования свободных процессоров из числа базовых, но другого типа, то достижение экстремума критерия (3.7) в общем случае не гарантируется.
При этом можно говорить не об оптимальном, а в той или иной степени близком к оптимальному решении проблемы распределения ресурсов. Соответствующий пример рассматривается в разделе 4 данной лекции.
Дата добавления: 2020-11-15; просмотров: 156; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!