Задания на тему «Числовые и степенные ряды»
1.1.Пользуясь необходимым признаком сходимости числовых рядов, доказать, что 
.
1.2. Найти область сходимости степенного ряда 
1.3. Вычислить приближенно 
с точностью до 
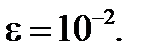
Задания на тему «Кратные и криволинейные интегралы»
2.1. Пластина задана неравенствами в декартовой системе координат 
– плотность материала, из которого изготовлена пластина. Найти массу пластины.
2.2. C помощью тройного интеграла вычислить объем тела, ограниченного поверхностями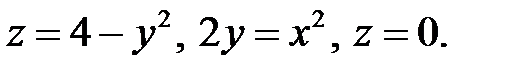 
Сделать чертежи данного тела и его проекции на координатную плоскость Oxy.
Задания на тему «Теория поля»
3.1. Даны скалярное поле 
точка 
и вектор 
Найти: а) скорость изменения скалярного поля U в точке А по направлению вектора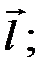 
б) наибольшую скорость возрастания U в точке А.
3.2. Доказать, что векторное поле 
потенциально, найти его потенциал. Выяснить, является ли поле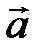 
соленоидальным.
3.3. Даны векторное поле 
поверхность 
и плоскость 
Найти: а) поток поля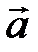 
через внешнюю сторону замкнутой поверхности 
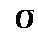, образованной поверхностью 
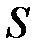и плоскостью Р; б) поток поля 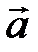через внешнюю сторону части поверхности 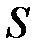, отсекаемой плоскостью Р; в) циркуляцию поля 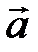вдоль контура, образованного пересечением поверхности 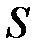и плоскости Р (направление обхода контура − положительное).
Вариант 2
Задания на тему «Числовые и степенные ряды»
1.1.Пользуясь необходимым признаком сходимости числовых рядов, доказать, что 
.
1.2. Найти область сходимости степенного ряда 
1.3. Вычислить приближенно 
с точностью 
Задания на тему «Кратные и криволинейные интегралы»
2.1. Пластина задана неравенствами в декартовой системе координат 
– плотность материала, из которого изготовлена пластина. Найти массу пластины.
2.2. C помощью тройного интеграла вычислить объем тела, ограниченного поверхностями 
Сделать чертежи данного тела и его проекции на координатную плоскость Oxy.
Задания на тему «Теория поля»
3.1. Даны скалярное поле 
точка 
и вектор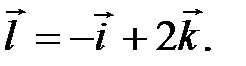 
Найти: а) скорость изменения скалярного поля U в точке А по направлению вектора 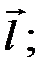б) наибольшую скорость возрастания U в точке А.
3.2. Доказать, что векторное поле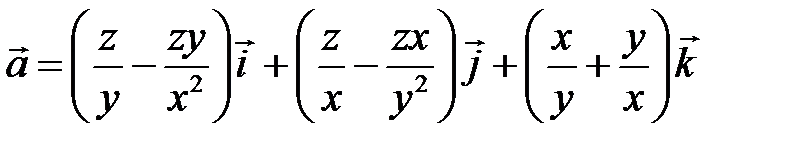 
потенциально, найти его потенциал. Выяснить, является ли поле 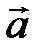соленоидальным.
3.3. Даны векторное поле 
поверхность 
и плоскость 
Найти: а) поток поля 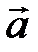через внешнюю сторону замкнутой поверхности s, образованной поверхностью 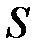и плоскостью Р; б) поток поля 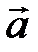через внешнюю сторону части поверхности 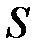, отсекаемой плоскостью Р; в) циркуляцию поля 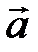вдоль контура, образованного пересечением поверхности и плоскости Р (направление обхода контура − положительное).
Вариант 3
Задания на тему «Числовые и степенные ряды»
1.1.Пользуясь необходимым признаком сходимости числовых рядов, доказать, что 
1.2. Найти область сходимости степенного ряда 
1.3. Вычислить приближенно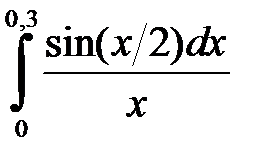 
с точностью 
Дата добавления: 2019-09-13; просмотров: 149; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!