Схеми додавання і віднімання сигналів
Точку з’єднання R1…Rm на інвертуючому вході можна вважати точкою Кірхгофа, в якій справджується І закон про суму струмів. Якщо окремо використовувати тільки по одному подільнику на інвертуючому та неінвертуючому вході, то одержимо диференційний каскад підсилення, в якому вихідна напруга буде визнчатись різницею напруг неінвертуючого та інвертуючого сигналів.
Uвих = Uвх.н – Uвх.і
Коли в каскаді буде виконуватись вимога пропорційності відповідних вхідних резистивних подільників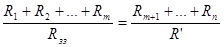 
, амплітуда вхідних сигналів на інвертуючому та неінвертуючому входах буде однаковою, то ми одержимо синфазні сигнали і вихідний сигнал буде рівний нулю. В протилежному випадку сигнали, які подаються на неінвертуючий вхід будуть додаватися, тобто ми одержимо найпростіший суматор; сигнали, що подаються на інвертуючий вхід є протифазними, тому вони теж додаються, але з протилежним знаком, таким чином одержимо схему віднімання сигналів. При наявності всіх диференційних сигналів реалізовується схема додавання та віднімання.
Інтегруючий підсилювач
Інтегруючий підсилювач – це каскад, в якому паралельний зворотний зв'язок задається за допомогою ємності конденсатора.
Ланка зворотного зв’язку реалізується у вигляді RC-кола. За І законом Кірхгофа справедливе співвідношення для струмів на інвертуючому колі:
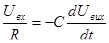
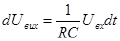
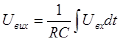
Вихідна напруга визначається як інтегральна функція від напруги на вході. Якщо на вході використати ланку резистивного суматора, тобто паралельно подати кілька вхідних сигналів через окремі резистори, то одержимо інтегруючий суматор:
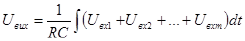
Диференціюючий каскад підсилення
Як і в попередньому випадку застосування І закону Кірхгофа дозволяє записати співвідношення струмів для інвертуючого входу:
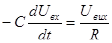
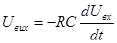
Таким чином в цьому каскаді одержимо як результат диференціювання вхідного сигналу. Застосування сумуючого входу дозволяє про диференціювати кілька сигналів:
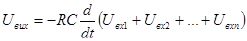
Оскільки струм вхідного кола є лінійною суперпозицією вхідних струмів.
Логарифмуючий підсилювач
Логарифмуючий підсилювач одержуємо при використанні в якості елемента зворотного зв’язку p-n переходу або бар’єру Шоткі. Це зумовлене тим, що зв'язок між напругою і струмом в p-n переході описується експоненційним законом:
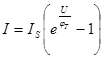
Тому за І законом Кірхгофа співвідношення струмів матиме вигляд:
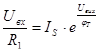
Якщо використовується пряма вітка ВАХ, логарифмування останнього співвідношення приводить до виразу:
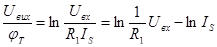
Таким чином з точністю до постійної інтегрування можна вважати, що вихідний сигнал є пропорційним натуральному логарифму вхідного сигналу.
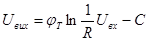
Використовуючи багатовходовий логарифматор можна реалізувати логарифмування суми сигналів:
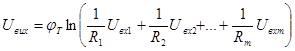
Антилогарифмуючий підсилювач
Зворотній зв'язок реалізується з допомогою лінійного елементу (резистора), а вхідний сигнал подається через нелінійний елемент. Тому співвідношення струмів на інвертуючому вході має вигляд: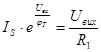 
.
В результаті вихідна напруга є експоненційною функцією вхідного сигналу:
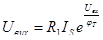
Використання кількох нелінійних входів дозволяє реалізувати суму експоненційних сигналів:
.
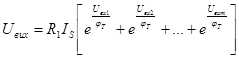Дата добавления: 2019-07-15; просмотров: 244; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!