О порядках силовских подгрупп общей линейной группы
В заметке (1) исправлена ошибка, допущенная Бернсайдом в работе (2). А именно в (3) доказано, что группа  порядка
порядка  , где
, где 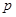 и
и 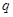 - различные простые числа и
- различные простые числа и 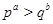 , либо обладает характеристической
, либо обладает характеристической 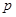 -подгруппой порядка
-подгруппой порядка  , либо справедливо одно из следующих утверждений:
, либо справедливо одно из следующих утверждений:
1) 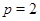 ,
, 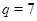 ,
, 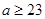 и
и  ;
;
2) 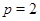 ,
, 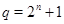 ,
,  и
и  , если
, если 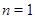 ,
,  , если
, если  ;
;
3) 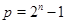 ,
, 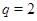 ,
, 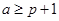 и
и 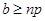 .
.
Доказательство этого результата сводится к случаю, когда силовская 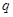 -подгруппа из
-подгруппа из  является минимальной инвариантной подгруппой, совпадающей со своим централизатором. В этом случае силовская
является минимальной инвариантной подгруппой, совпадающей со своим централизатором. В этом случае силовская  - подгруппа из
- подгруппа из  изоморфно вкладывается в общую линейную группу
изоморфно вкладывается в общую линейную группу  и возникает необходимость сравнить порядок силовской
и возникает необходимость сравнить порядок силовской 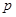 -подгруппы из
-подгруппы из  с числом
с числом  . В лемме 2.5 из указывались значения
. В лемме 2.5 из указывались значения 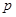 ,
,  и нижняя граница для числа
и нижняя граница для числа 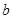 , при которых порядок силовской
, при которых порядок силовской  - подгруппы из
- подгруппы из  больше
больше  .
.
Цель настоящей заметки - указать все значения чисел 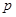 ,
, 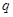 и
и  , при которых силовская
, при которых силовская  -подгруппа из
-подгруппа из  имеет порядок больший, чем
имеет порядок больший, чем  .
.
Теорема Пусть 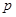 и
и  - различные простые числа и
- различные простые числа и 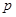 - порядок силовской
- порядок силовской 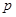 -подгруппы из группы
-подгруппы из группы  . Тогда и только тогда
. Тогда и только тогда  , когда выполняется одно из условий:
, когда выполняется одно из условий:
1) 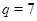 ,
,  ,
, 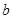 - любое натуральное число за исключением
- любое натуральное число за исключением  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ;
;
2) 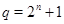 ,
,  ,
, 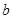 - любое натуральное число
- любое натуральное число  ;
;
3) 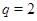 ,
,  ,
, 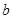 - любое натуральное число
- любое натуральное число  за исключением
за исключением  , где
, где  ;
;  , где
, где 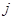 - любое целое число, удовлетворяющее неравенству
- любое целое число, удовлетворяющее неравенству  . Для
. Для  дополнительно исключаются числа
дополнительно исключаются числа  ,
,  ,
,  и
и  ; для
; для  дополнительно исключаются
дополнительно исключаются  и
и  .
.
|
|
|
Доказательство теоремы основывается на формуле для вычисления порядка силовской  -подгруппы общей линейной группы
-подгруппы общей линейной группы  , полученной в .
, полученной в .
Пусть 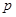 и
и  - различные простые числа,
- различные простые числа, 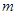 - показатель числа
- показатель числа 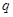 по модулю
по модулю 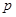 и
и  ,
,  не делит
не делит 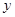 . Через
. Через  обозначим порядок силовской
обозначим порядок силовской  -подгруппы группы
-подгруппы группы  , а через
, а через  - показатель, с которым
- показатель, с которым 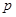 входит в произведение
входит в произведение  . В доказана следующая
. В доказана следующая
Лемма Если  , то
, то  . Если
. Если  , то
, то  и число
и число  определяется так: пусть
определяется так: пусть  - наименьшее целое, при котором
- наименьшее целое, при котором  и
и  ; если
; если  , то
, то  ; если
; если  , то
, то  ,
,  - нечетное число.
- нечетное число.
Напомним, что  - целая часть числа
- целая часть числа  , т.е. наибольшее целое число, не превосходящее
, т.е. наибольшее целое число, не превосходящее  (см. ).
(см. ).
Лемма Если  - натуральное число, то
- натуральное число, то

Доказательство. Пусть  - наибольшее целое число, при котором
- наибольшее целое число, при котором  . Так как
. Так как  , то
, то

С другой стороны,
 и
и  .
.
Лемма Если  - натуральное число
- натуральное число  , то
, то  .
.
Доказательство проводим индукцией по 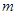 . Если
. Если  , то
, то

Пусть утверждение верно для  . Докажем его для
. Докажем его для  .
.
Если 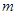 кратно
кратно  , то
, то
 . Но
. Но  - целое число, а
- целое число, а  -
-
дробное. Поэтому

Если  кратно
кратно  , то
, то  .
.
Пусть, наконец, оба числа  и
и  не кратны
не кратны  , тогда
, тогда  , причем
, причем  не целое число. Так как число
не целое число. Так как число  целое, то
целое, то  , откуда
, откуда  . Лемма доказана.
. Лемма доказана.
Лемма Если  - натуральное число, а
- натуральное число, а  - наибольшее целое число, при котором
- наибольшее целое число, при котором  , то
, то  .
.
|
|
|
Доказательство. По лемме ,  , поэтому
, поэтому  . Неравенство
. Неравенство  докажем индукцией по
докажем индукцией по  . Для
. Для  и
и  справедливость неравенства проверяется непосредственно.
справедливость неравенства проверяется непосредственно.
Пусть  и пусть это неравенство верно для всех
и пусть это неравенство верно для всех  . Докажем его для
. Докажем его для  . Разность
. Разность  обозначим через
обозначим через  . Так как
. Так как  , то
, то  . Поэтому если
. Поэтому если  - наибольшее целое число, при котором,
- наибольшее целое число, при котором,  , то
, то  и по индукции имеем
и по индукции имеем 
Вычислим  . Так как
. Так как

то

Лемма доказана.
Замечание. Границы, указанные в лемме , точные. Левая граница достигается при  , правая - при
, правая - при  .
.
Лемма Если натуральное число  , то
, то  и
и  .
.
Доказательство обоих неравенств легко получить индукцией по  .
.
Доказательство теоремы 3. Сохраним все обозначения леммы . Рассмотрим вначале случай, когда  . По лемме (5), в этом случае
. По лемме (5), в этом случае  , где
, где  . Допустим, что
. Допустим, что  . Так как
. Так как  , то
, то  и
и  . Поэтому
. Поэтому  , и, применяя лемму , получаем
, и, применяя лемму , получаем  , что противоречит условию теоремы.
, что противоречит условию теоремы.
Значит,  , поэтому либо
, поэтому либо  , либо
, либо 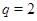 .
.
Пусть  . Тогда
. Тогда  , а так как
, а так как  , то
, то  и
и  .
.
Пусть 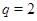 . Тогда
. Тогда  . Если
. Если  четное, то
четное, то  , т.е.4 делит
, т.е.4 делит  . Противоречие. Значит,
. Противоречие. Значит,  нечетное. Поэтому
нечетное. Поэтому  , и так как число
, и так как число  нечетное, то
нечетное, то  . Таким образом, если
. Таким образом, если 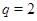 , то
, то  .
.
Итак, если  , то либо
, то либо  и
и  , либо
, либо 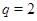 и
и  .
.
Пусть  . Тогда из леммы следует, что
. Тогда из леммы следует, что

Предположим, что  . Тогда
. Тогда  (см. лемму ), а так как при
(см. лемму ), а так как при  справедливо неравенство
справедливо неравенство  , то
, то  . Учитывая, что
. Учитывая, что  или
или  , получаем
, получаем  .
.
|
|
|
Если  , то
, то  и
и  . Кроме того,
. Кроме того,  , поэтому
, поэтому
 и
и  .
.
Таким образом, при  выполняется неравенство
выполняется неравенство  . Так как
. Так как  , то
, то  . Противоречие с условием теоремы.
. Противоречие с условием теоремы.
Следовательно,  или
или  и
и  или
или  .
.
Итак, нам необходимо рассмотреть следующие случаи:  ,
,  ;
;  ,
,  ;
; 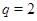 ,
,  .
.
Случай 1. Пусть 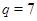 ,
,  . В этом случае
. В этом случае

Если  , то, вычисляя
, то, вычисляя  для каждого значения
для каждого значения  с помощью натуральных логарифмов, убеждаемся; что
с помощью натуральных логарифмов, убеждаемся; что  в точности для следующих
в точности для следующих  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  --
--  ,
,  --
--  .
.
Пусть  и
и  - наибольшее натуральное число, при котором
- наибольшее натуральное число, при котором  . Ясно, что
. Ясно, что  . С помощью индукции легко проверяется неравенство;
. С помощью индукции легко проверяется неравенство;  . Используя лемму , мы получаем:
. Используя лемму , мы получаем:

Теперь
 Таким образом,
Таким образом,  .
.
Случай 2. Пусть  ,
,  . В этом случае
. В этом случае  , где
, где  , если
, если  четное, и
четное, и  если
если  нечетное, а
нечетное, а  . Если
. Если  или 3, а
или 3, а  , то непосредственно убеждаемся, что
, то непосредственно убеждаемся, что  . Если
. Если  , то
, то  , а
, а  и
и  т.е.
т.е.  . Используя лемму , получаем
. Используя лемму , получаем
 т.е.
т.е. 
Теперь пусть  . Из леммы имеем
. Из леммы имеем  или
или  . Поэтому
. Поэтому  . Осталось рассмотреть случай, когда
. Осталось рассмотреть случай, когда  . Тогда
. Тогда  , поэтому, используя леммы и , получаем:
, поэтому, используя леммы и , получаем:

Таким образом, при любом  имеет место неравенство
имеет место неравенство  .
.
Случай 3. Пусть 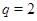 ,
,  . В этом случае
. В этом случае  , где
, где  - целая часть числа
- целая часть числа  . Если
. Если  , то
, то  и
и  . Отсюда следует, что
. Отсюда следует, что  . Противоречие. Значит,
. Противоречие. Значит,  и
и  . Мы можем записать
. Мы можем записать  ,
,  .
.
|
|
|
Рассмотрим вначале случай, когда  , т.е. когда
, т.е. когда  .
.
Тогда  ,
,  .
.
Если  , то
, то  , где
, где  - основание натуральных логарифмов и
- основание натуральных логарифмов и
 , т.е.
, т.е.  .
.
Если  , то
, то  и
и  , т.е.
, т.е.  . Найдем значения
. Найдем значения  для
для  и
и  . Для
. Для  имеем:
имеем:

Для  имеем:
имеем:

Если  , то
, то  , и при
, и при  получаем
получаем
 , т.е.
, т.е.  .
.
Если  , то
, то  . Определим для
. Определим для  и
и  значения
значения  , при которых
, при которых  . Для
. Для  имеем
имеем  , т.е.
, т.е.  , а
, а  . Для
. Для  имеем
имеем  , т.е.
, т.е.  , а
, а  .
.
Теперь рассмотрим случай, когда  , т.е. когда
, т.е. когда  .
.
Если  , то
, то  и
и  . Непосредственно убеждаемся, что лишь при
. Непосредственно убеждаемся, что лишь при  или
или  имеет место неравенство
имеет место неравенство  .
.
Если  , то
, то  и
и  . Непосредственно убеждаемся, что лишь только при
. Непосредственно убеждаемся, что лишь только при  и
и  имеет место неравенство
имеет место неравенство  .
.
Пусть  . Так как
. Так как  , a
, a  , то
, то
 ,
,
так как  .
.
Таким образом,  .
.
Пусть теперь  . Тогда
. Тогда  . Пусть вначале
. Пусть вначале  . Тогда
. Тогда  , и по лемме 3 имеем
, и по лемме 3 имеем  . Поэтому
. Поэтому

Здесь мы воспользовались неравенством  , которое вытекает из неравенства
, которое вытекает из неравенства  . Таким образом, доказано, что
. Таким образом, доказано, что  .
.
Остался случай  . Так как
. Так как  , то
, то

и, применяя лемму , получаем

Таким образом,  .
.
Теорема доказана.
Заключение
Итак, в данной курсовой работе исследовано существование примарных нормальных подгрупп в бипримарных группах. Также изучены и доказаны следующие основные теоремы:
Теорема. Пусть  - конечная разрешимая группа, порядка
- конечная разрешимая группа, порядка  ,
,  - простое число и
- простое число и  не делит
не делит  . Если
. Если  , то либо
, то либо  обладает характеристической
обладает характеристической  -подгруппой порядка
-подгруппой порядка  , либо справедливо одно из следующих утверждений:
, либо справедливо одно из следующих утверждений:
1)  ,
,  и
и  делит порядок
делит порядок  ;
;
2)  ,
,  делит порядок
делит порядок  , где
, где  - простое число, причем
- простое число, причем  , если
, если  , и
, и  , если
, если  ;
;
3)  ,
,  1 и
1 и 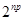 делит порядок
делит порядок  .
.
Теорема. Пусть  - группа порядка
- группа порядка  ,
,  и
и  - простые числа. Если
- простые числа. Если  , то либо
, то либо  обладает характеристической
обладает характеристической  -подгруппой порядка
-подгруппой порядка  , либо справедливо одно из следующих утверждений:
, либо справедливо одно из следующих утверждений:
1)  ,
,  ,
,  и
и  ;
;
2)  ,
,  ,
,  , причем
, причем  , если
, если  , и
, и  , если
, если  ;
;
3)  ,
,  ,
,  и
и  .
.
Теорема. Группа порядка 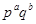 ,
,  , не имеющая неединичных инвариантных
, не имеющая неединичных инвариантных  -подгрупп, существует для каждого из следующих трех случаев:
-подгрупп, существует для каждого из следующих трех случаев:
1)  ,
,  ,
,  и
и  ;
;
2)  ,
,  ,
,  и
и  , если
, если  ,
,  , если
, если  ;
;
3)  ,
,  ,
,  и
и  .
.
Теорема. Пусть  и
и 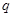 - различные простые числа и
- различные простые числа и  - порядок силовской
- порядок силовской  -подгруппы из группы
-подгруппы из группы  . Тогда и только
. Тогда и только 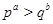 , когда выполняется одно из условий:
, когда выполняется одно из условий:
1) 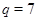 ,
, 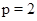 ,
,  - любое натуральное число за исключением
- любое натуральное число за исключением  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ;
;
2)  ,
,  ,
,  - любое натуральное число
- любое натуральное число  ;
;
3)  ,
,  ,
,  - любое натуральное число
- любое натуральное число  за исключением
за исключением  , где
, где  ;
;  , где
, где  - любое целое число, удовлетворяющее неравенству
- любое целое число, удовлетворяющее неравенству  . Для
. Для  дополнительно исключаются числа
дополнительно исключаются числа  ,
,  ,
,  и
и  ; для
; для  дополнительно исключаются
дополнительно исключаются  и
и  .
.
Список литературы
Burnside W., On groups of order  , Proc. London Math. Soc.2, № 1 (1904), 388--392.
, Proc. London Math. Soc.2, № 1 (1904), 388--392.
Вurnside W., On groups of order  (Second paper), Proc. London Math. Soc., 2, № 2 (1905), 432--437.
(Second paper), Proc. London Math. Soc., 2, № 2 (1905), 432--437.
Вurnside W., Theory of groups of finite order, Cambridge, 1911.
Виноградов И.М., Основы теории чисел, М., Наука, 1965.
Huppert В., Endliche Gruppen. I, Berlin, Springer, 1967.
Шеметков Л.А., К теореме Д.К. Фаддеева о конечных разрешимых группах, Матем. заметки, 5, № 6 (1969), 665--668.
Монахов В.С., Инвариантные подгруппы бипримарных групп. Матем. заметки, 18, № 6 (1975) б 877-886.
Burnside W., On groups of order  (second paper), Proc. London Math. Soc., 2, N 2 (1905), 432--437.
(second paper), Proc. London Math. Soc., 2, N 2 (1905), 432--437.
Виноградов И.М., Основы теории чисел, М., 1965.
Дата добавления: 2019-07-15; просмотров: 97; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
