Описание напряженного состояния твердых тел

 

Напряженное состояние в точке твердого тела в прямоугольной системе координат описывается шестью компонентами напряжений, действующих на гранях элементарного куба, вырезанного в окрестностях рассматриваемой точки. При этом нормальные напряжения σ перпендикулярны граням куба, а касательные τ – действуют в плоскости граней куба. Ориентацию граней куба можно подобрать так, что величины τ окажутся равными нулю. Т.е. вектор напряжения p будет перпендикулярен рассматриваемой грани. Действующие в этом случае нормальные напряжения называют главными нормальными напряжениями и обозначают σ1, σ 2 и σ3. Ориентация главных напряжений показана на рисунке 4.1 а. Главные касательные напряжения действуют на диаго-нальных поверхностях элементарного куба и соответственно равны

 

τ₁ = 0,5(σ₃ – σ₂);
τ₂ = 0,5(σ₃ – σ₁);                                   (4.1)

τ₃ = 0,5(σ₂ – σ₁),

 

где τ1, τ2 и τ3 – главные касательные напряжения. Отличительной особенно-стью главных напряжений является то, что одно из них максимальное и одно – минимальное по величине.

 

 

Рис. 4.1. Компоненты главных напряжений в прямоугольных (а) и цилиндрических (б) координатах

 

Расчет стенок скважины принято вести в цилиндрической системе коор-динат . Аппликату (ось z) совмещают с осью скважины , как показано на рис. 4.1 б. Компоненты нормальных напряжений обозначают соответственно: в направлении оси z – напряжение σ_z, в направлении радиус-вектора r – напряжение σ_r (радиальное напряжение) и в направлении, перпендикулярном радиус-вектору–σt(тангенциальное напряжение).Формулы для расчета главных касательных напряжений аналогичны формулам (4.1).

Для упрощения описания напряженного состояния твердых тел широко используют приведенные (эквивалентные) напряжения, называемые интенсивностью касательных напряжений и обозначаемые буквой σ_i, и среднее нормальное напряжение σ₀, соответственно равные

 

                 ;           (4.2)
                                                                                (4.3)

 

Таким образом, для описания напряженного состояния твердого тела ни-же будут использованы три компоненты главных нормальных напряжений и три компоненты главных касательных напряжения или интенсивность каса-тельных напряжений и среднее нормальное напряжение.

 

Основные модели твердых тел

 

Для удобства математического описания все твердые тела делят на группы, для каждой из которых создается идеализированная математическая модель, включающая лишь наиболее существенные признаки группы. Модель представляет собой зависимость деформации от напряжения. Все модели делятся на простые (основные) и сложные. Сложные модели представляют собой комбинации простых моделей. Основные модели твердых тел следующие:

1. Идеальное упругое тело или тело Гука,деформация которого прямопропорциональна соответствующему напряжению. На рисунке 4.2 а приведены схема деформирования куба единичных размеров и график соответствующей зависимости γ от τ. При рассмотрении всех моделей использованы деформации сдвига и касательные напряжения, тогда

 

(4.4)

 

где γ – деформация сдвига; τ – касательные напряжения; G – модуль деформации (упругости) при сдвиге.

2. Идеальное упругопластическое тело (рис. 4.2б)деформируется упругов области  <  , где   – касательные напряжения, соответствующие пределу текучести материала куба, а при  <  деформируется пластически при постоянных напряжениях (  <  = const, 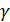 → ∞ ). Один из механизмов пластического деформирования заключается в следующем. По мере увеличения напряжения в плоскостях с наибольшей концентрацией дефектов структурыматериала формируются площадки скольжения и далее при τ = τs происходит скольжение одних частей материала относительно других без нарушения сплошности.

 

 

Рис. 4.2. Схемы деформирования простых моделей твердых тел и графики зависимости  для них

3.Идеальное жесткопластическое тело (рис. 4.2в).Если пластическая деформация   много больше упругой  , то при решении задач принимает-

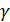= 0, тогда при  <  =  = 0, а при  =  =  → ∞ .

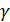4. Упругопластическое упрочняющееся тело (рис. 4.2г)отличается отидеального упругопластического тела только тем, что при  >  для при-ращения пластической деформации необходимо увеличивать напряжения.

5. Вязкое тело, или тело Ньютона (рис. 4.2д),описывает зависимость скорости деформирования от напряжения и вязкости вещества, а именно

                                           (4.5)

где t – время; η – коэффициент вязкости вещества твердого тела.

В уравнения моделей твердых тел входят как переменные величины γ и τ, так и постоянные коэффициенты или величины, например G, τs, η , отражающие проявление тех или иных механических свойств твердого тела и принимаемые качестве показателей этих свойств. В соответствии с видами моделей выделяют группы упругих, пластических, реологических (вязкостных) и прочностных показателей механических свойств твердых тел.

Следует помнить, что показатели механических свойств твердых тел или, частности, горных пород нельзя определить вне условий, накладываемых опытом. Поэтому показатели свойств не эквивалентны свойствам, а лишь отражают их проявление в условиях опыта. Для того чтобы показатели механических свойств были сопоставимы, методы и условия их определения стандартизованы.

 

Обобщенный закон Гука

 

Закон Гука описывает деформирование твердых тел в упругой области нагружения. Особенности деформирования при действии только нормального и одновременно нормального и касательного напряжений показаны на рисунке 4.3. В окрестности рассматриваемой точки выделен элемент твердого тела в виде куба с длиной ребра l. Под действием напряжения σ_z (одноосное растяжение) элемент увеличился в длину на величину l_z, но стал уже и тоньше на вели-чину l_х (рис. 4.3 а). Продольная деформация σ_z в соответствии с законом Гука

(4.6)

 

где Е –модуль деформации(упругости)при растяжении/сжатии(модуль Юн-га). Поперечная деформация ε_x , равная

 

прямо пропорциональна величине εz, т.е.
	(4.7)
где μ – модуль поперечной деформации (коэффициент Пуассона).

 

а                                                               б

 

Рис. 4.3. Схемы деформирования элемента твердого тела

 

При одновременном действии нормального σz и касательного напряжения τxy элемент изменит не только размеры, но и форму за счет деформации сдвига на величину γ (рис. 4.3 б).

В общем случае на всех гранях выделенного куба могут действовать как нормальные напряжения σz, σх и σу, так и касательные τху, τxz и τzy.

На рис. 4.3 б показан частный случай, когда нормальные и касательные напряжения действуют только на гранях куба, перпендикулярных оси z. При этом имеют место нормальные деформации, как продольные, так и поперечные:

 

ε_z' = σ_z /Е; ε_x' = –με_z; ε_y' = –με_z,

 

а также деформация сдвига γ xz = τxz /G, где G – модуль деформации ( упругости) при сдвиге. Соответственно , под действием напряжений на гранях куба, перпендикулярных только оси х и оси у, будут иметь место деформации:

εx'' = σx /Е; εy'' = –μεx; εz'' = -μεx; γxy = τxy /G;
εy''' = σy /Е; εx''' = –μεy; εz''' = -μεy; γyz = τyz /G.

Полная деформация от действия напряжений на всех гранях будет равна частным деформациям в направлении соответствующей оси. Например, в на-правлении оси z:

εz = εz' + εz'' + εz''' =	1	[εz – μ(εx + εy )].	(4.8)
	Е

Аналогично проведем суммирование по направлениям х и у.

Под действием напряжений изменяются не только размеры и форма тела, но и его объем. При этом объемная деформация ε_v обратно пропорциональна среднему нормальному напряжению σ_o:

ε_v = σ_o /К,

где К – модуль объемной деформации.

В итоге получаем систему из семи уравнений, связывающих напряжения деформации выделенного элемента твердого тела:

 

 

1			[εz – μ(εx + εy )];		γxz = τxz /G;
Е
1				[εx – μ(εz + εy )];	γxy = τxy /G;	(4.9)
	Е
1			[εy – μ(εz + εx )];		γyz = τyz /G;
Е

          ε_v = σК₀ = 31К (σ_z + σ_x + σ_y).

 

Система уравнений(4.9) получила название обобщенный закон Гука. Для идеально упругого тела

 

G =		Е		:		(4.10)
		2(1 − μ )
K =		Е			.	(4.11)
	3(1 − 2μ )

 

Величина, обратная модулю объемной деформации, соответствует коэффициенту сжимаемости β твердого тела, т.е.

 

β = 1/К,

(4.12)

 

где β – коэффициент сжимаемости.

Из уравнений (4.6), (4.10) и (4.11) видно, что основными упругими характеристиками твердого тела являются модуль Юнга и коэффициент Пуассона. Полученные уравнения справедливы только для идеально упругого изотропного тела. В природе же часто приходится иметь дело с анизотропными неодно-родными телами, что существенно осложняет их математическое описание. Для того чтобы избежать этих трудностей, вводят ряд допущений и ограничений (например, для горных пород закономерности деформирования, полученные для условий сжатия, нельзя распространять на условия растяжения), что делает возможным использование уравнений (4.9) для описания механических процес-сов в реальных твердых телах.

 

---

Дата добавления: 2019-02-22; просмотров: 662; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!