Елементарні перетворення системи лінійних рівнянь
| 1) | додавання до обох частин рівняння відповідних частин другого, помножених на одне число; |
| 2) | переставлення рівнянь місцями; |
| 3) | виключення з подальшого розгляду рівнянь, що є тотожностями для всіх значень невідомих змінних. |
Ці елементарні перетворення не змінюють сумісності і розв’язку системи лінійних рівнянь.
Умову сумісності системи лінійних рівнянь характеризує теорема Кронекера-Капеллі (Леопольд Кронекер (1823-1891) ‑ німецький математик).
| Теорема 1.4. (Кронекера-Капеллі) | Для того, щоб система лінійних алгебраїчних рівнянь (1.8) була сумісною, необхідно і достатньо, щоб ранг матриці  системи (1.8) дорівнював рангу розширеної матриці  системи (1.8).
|
| Приклад 1.6. | Перевірити сумісність системи рівнянь
|
Розв’язання. Випишемо основну та розширену матриці системи лінійних рівнянь: 
, 
.
З елементів цих двох матриць можна скласти базисний мінор третього порядку, що не дорівнює нулю: 
.
Отже, 
і 
. Тобто 
. За теоремою Кронекера-Капеллі досліджувана система лінійних рівнянь є сумісною.
Частинним випадком прямокутної системи (1.8) є квадратна система рівнянь 
. Тоді матриця системи 
є квадратною:
,
а її визначник 
називають основним визначником системи.
Метод Крамера
Метод Крамера (Габріель Крамер (1704-1752) ‑ швейцарський математик) застосовують до знаходження розв’язку квадратних систем лінійних рівнянь. В ньому застосовують поняття визначника основної матриці системи 
і допоміжних визначників 
, які отримують з визначника 
заміною першого, другого і так далі до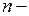 
го стовпця на стовпець вільних членів:
, 
, …, 
.
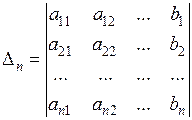Наприклад, для системи, що містить три лінійних рівняння з трьома невідомими
,
маємо: 
, 
, 
, 
.
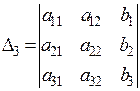В залежності від значення визначника основної матриці та значень допоміжних визначників реалізується один з трьох варіантів:
| 1) | Якщо визначник основної матриці системи (1.8) не дорівнює нулю  , то система (1.8) має єдиний розв’язок, який знаходять за формулами Крамера:
 . (1.10)
|
| 2) | Якщо основний визначник системи (1.8) дорівнює нулю  і всі допоміжні визначники теж дорівнюють нулю  , тоді система (1.8) має безліч розв’язків.
|
| 3) | Якщо основний визначник системи (1.8) дорівнює нулю, а хоча б один з допоміжних визначників   не дорівнює нулю, тоді система не має жодного розв’язку.
|
Слід зауважити, що метод Крамера для випадку 2 тільки встановлює існування нескінченної множини розв’язків, але не дає їх виду.
Для однорідної системи лінійних рівнянь при 
система має єдиний розв’язок 
. При 
однорідна система має безліч розв’язків.
| Приклад 1.7. | Розв’язати систему лінійних рівнянь методом Крамера
|
Розв’язання. Визначник основної матриці системи має вид 
. Оскільки він відрізняється від нуля, робимо висновок про існування єдиного розв’язку системи.
Обчислимо допоміжні визначники:
, 
, 
.
За методом Крамера згідно формул (1.10) маємо розв’язок:
.
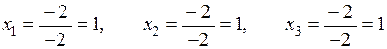Після знаходження розв’язку системи лінійних рівнянь рекомендується провести перевірку правильності проведених обчислень.
Перевірка: підстановка у вихідну систему одержаних значень невідомих 
, 
, 
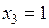призводить до тотожностей: 
що підтверджує правильність отриманого результату.
Метод оберненої матриці
Матричний метод засновано на використанні властивостей множення матриць. Цей метод є дуже зручним у випадку систем невисокого порядку.
Якщо основна матриця 
системи (1.8) є невиродженою, тобто 
, тоді для неї існує обернена 
. Помножимо матричну рівність (1.9) зліва на обернену матрицю :
. (1.11)
З відношення (1.11) з урахуванням відомої формули 
, а також властивостей множення матриць, а саме 
, випливає матрична форма розв’язку системи (1.8):
. (1.12)
Співвідношення (1.11) лежить в основі методу оберненої матриці.
| Приклад 1.8. | Розв’язати систему лінійних рівнянь з прикладу 1.7 методом оберненої матриці. |
Розв’язання. Для основної матриці системи 
, яка є невиродженою, оскільки 
, обернена буде такою:
.
Вектор-стовпець вільних членів є таким: 
. Тоді за формулою (1.12) одержимо: 
.
Отже, 
.
| Приклад 1.9. | Розв’язати матричним методом систему лінійних рівнянь 
|
Розв’язання. Знайдемо обернену до матриці 
з визначником 
: 
.
Тоді 
.
Отже, 
.
Незважаючи на обмеження можливості застосування методу оберненої матриці і складність обчислень при великих значеннях коефіцієнтів, а також систем високого порядку, матричний метод може бути легко реалізованим на ЕОМ.
Метод оберненої матриці і метод Крамера є дуже трудомісткими за кількістю обчислювальної роботи. Тим часом існують більше економічні методи розв’язання систем лінійних рівнянь, які опираються на попереднє перетворення матриці системи до спеціального виду. Одним із них є метод Гауса, що застосовується не тільки у випадку, коли 
.
Метод Гаусса
Метод Гаусса – метод послідовного виключення змінних – полягає в тому, що за допомогою елементарних перетворень система рівнянь шляхом послідовного виключення змінних приводиться до рівносильної системи східчастого (або трикутного) виду, з якої, починаючи з останніх (за номером) змінних, знаходять всі інші змінні.
Метод Гаусса є універсальним методом розв’язання систем лінійних рівнянь (1.8). Метод Гаусса реалізується в два етапи, які розділяються на декілька кроків. Перший етап полягає у приведенні системи лінійних рівнянь до трикутного вигляду.
І етап - прямий хід виключень:
І крок - припустимо, що коефіцієнт 
(у протилежному випадку можна поміняти місцями рівняння у системі). Поділимо перше рівняння на 
і за його допомогою виключимо з усіх інших рівнянь системи змінну 
. Для цього слід одержане перше рівняння помножити на 
, …, 
та додати відповідно до другого, … , т-го рівнянь системи. Таким чином одержимо еквівалентну вихідній систему лінійних рівнянь, яка містить змінну 
тільки у першому рівнянні.
ІІ крок - перше рівняння залишаємо без змін. Далі припустимо, що коефіцієнт при 
у другому рівнянні одержаної системи відрізняється від нуля. Слід розділити на нього друге рівняння і аналогічно першому кроку виключити змінну 
з усіх рівнянь системи. Змінна , таким чином, залишається тільки в першому та другому рівняннях.
ІІІ крок - Перше і друге рівняння залишаються без змін. За основу беруть третє рівняння і за його допомогою виключають змінну 
.
Процес послідовного виключення змінних продовжується до приведення вихідної системи лінійних рівнянь до системи лінійних рівнянь трикутного вигляду:
(1.13)
де 
, 
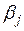- нові коефіцієнти при невідомих.
Другий етап передбачає знаходження значень невідомих з одержаної системи рівнянь, проводячи рух у протилежному напрямку.
ІІ етап - обернений хід методу Гаусса:
І крок - з останньої рівності модифікованої системи визначаємо вираз змінної 
через змінні 
, … , 
.
ІІ крок - з передостанньої рівності визначаємо вираз змінної 
через змінні , … , 
з урахуванням виразу змінної 
.
Далі проводяться аналогічні перетворення для знаходження виразу всіх інших змінних до 
. В результаті подібних розрахунків одержимо
(1.14)
Невідомі 
називають базисними змінними, а невідомі 
називають вільними змінними.
Ранг основної матриці системи (1.8) дорівнює кількості базисних змінних.
Розглянемо застосування цього методу на конкретному прикладі.
| Приклад 1.10. | Розв’язати методом Гаусса систему лінійних рівнянь: 
|
Розв’язання. Перший етап: приведемо вихідну систему до трикутного вигляду. Перше і третє рівняння поміняємо місцями і розділимо перше рівняння на 
:
Перше рівняння перепишемо без змін. Помножимо перше рівняння на 
та 
і додамо до другого та третього рівнянь:
Третє рівняння розділимо на 10 і поміняємо місцями з другим:
Перше і друге рівняння перепишемо без змін. Друге рівняння помножимо на 
і додамо до третього:
Другий етап: знайдемо значення невідомих. З останньої рівності одержимо 
і підставимо у друге рівняння, з якого визначимо 
. Підставимо значення і 
в перше рівняння системи і одержимо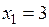 
. Отже, розв’язок вихідної системи є таким: 
, 
, 
.
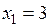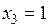На практиці зручним виявляється застосовувати ідею методу Гаусса для перетворення елементів розширеної матриці системи лінійних рівнянь, а не до самих рівнянь. Така модифікація методу Гаусса заснована на використанні правила прямокутника.
Прямий хід методу Гаусса, тобто приведення розширеної матриці 
до трикутного вигляду, реалізується згідно наступного алгоритму.
Дата добавления: 2019-02-13; просмотров: 612; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!