Спектральное представление сигналов.

⇐ ПредыдущаяСтр 2 из 2

Совокупность гармонических составляющих, образующих негармонический сигнал, называется спектром этого сигнала. Спектр можно было бы представить графически в виде совокупности временных кривых входящих в него гармоник, но такое изображение громоздко и малонаглядно, поэтому не используется. Вместо этого принято изображать спектр сигнала в виде линейчатой диаграммы, в которой на оси частот наносятся вертикальные отрезки, длина которых пропорциональна амплитуде данной гармоники, а её положение на оси частот определяется номером гармоники. Например, если некоторый периодический сигнал описывается рядом

, то спектр этого сигнала представляет рис.12.

100

w₁ 2w₁ 3w₁ w

рис. 12

На этом спектре показаны соотношения амплитуд спектральных составляющих сигнала, поэтому спектр называется амплитудным. Аналогично можно строить фазные спектры, на которых по оси частот откладывают начальные фазы гармоник также в виде вертикальных отрезков в выбранном масштабе.

Так как ряд любого периодического сигнала состоит из гармоник, частоты которых в целое число раз отличаются от частоты первой гармоники, то спектральные линии находятся на одинаковом расстоянии Dw друг от друга (или D¦), которое равно частоте основной гармоники w₁ (или ¦₁). Спектры, состоящие из отдельных линий, называются дискретными или линейчатыми.

Приведем примеры спектров некоторых рассмотренных нами сигналов. Из (21) следует, что сигналы треугольной формы состоят из гармоник с нечетными номерами, амплитуды которых убывают пропорционально квадрату номера гармоники. Амплитуды в спектрах можно строить в относительных единицах. Если принять амплитуду первой гармоники за 1, то амплитуда второй гармоники , амплитуда 3-й гармоники в 1/3² меньше, чем первой, т.е. 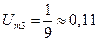, , 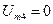и т.д. Спектр этого сигнала на рис. 13.

0,11

0,04

¦₁ 2¦₁ 3¦₁ 4¦₁ 5¦₁ ¦

рис. 13

Из (22) спектр сигналов прямоугольной формы со скважностью 2 состоит из нечетных гармоник, амплитуды которых убывают пропорционально номерам гармоник. Поэтому амплитуды всех четных гармоник также равны нулю, а амплитуды нечетных гармоник по отношению к амплитуде первой гармоники, принятой за 1, будут выражаться: ; ; …… Спектр на рис. 14

0,33

0,2

¦₁ 2¦₁ 3¦₁ 4¦₁ 5¦₁ ¦

рис. 14

Спектры последовательности прямоугольных импульсов.

Рассмотрим периодическую последовательность импульсов прямоугольной формы с периодом Т, длительностью импульсов и максимальным значением . Найдем разложение в ряд такого сигнала, выбрав начало координат как показано на рис. 15. при этом функция симметрична относительно оси ординат, т.е. все коэффициенты синусоидальных составляющих =0, и нужно рассчитать только коэффициенты .

U(t)

U_m

- 0 T t

Рис. 15

(27)

постоянная составляющая (28)

Постоянная составляющая – это среднее значение за период, т.е. это площадь импульса , деленная на весь период, т.е. 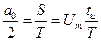, т.е. то же, что получилось и при строгом формальном вычислении (28).

Вспомним, что частота первой гармоники ¦₁= , где Т – период прямоугольного сигнала. Расстояние между гармониками D¦=¦₁. Если номер гармоники n окажется таким, что аргумент синуса , откуда . Номер гармоники, при котором амплитуда ее обращается в ноль первый раз, называют «первым нулем» и обозначают его буквой N, подчеркивая особые свойства этой гармоники:

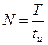(29)

с другой стороны, скважность S импульсов – это отношение периода Т к длительности импульсов t_u, т.е. . Следовательно «первый нуль» численно равен скважности импульса N = S. Поскольку синус обращается в ноль при всех значениях аргумента, кратных p, то и амплитуды всех гармоник с номерами, кратными номеру «первого нуля», тоже обращаются в ноль. То есть при , где k – любое целое число. Так, например, из (22) и (23) следует, что спектр прямоугольных импульсов со скважностью 2 состоит только из нечетных гармоник. Поскольку S =2, то и N =2, т.е. амплитуда второй гармоники первый раз обращается в ноль – это «первый нуль». Но тогда и амплитуды всех остальных гармоник с номерами, кратными 2, т.е. все четные тоже должны обращаться в ноль. При скважности S=3 нулевые амплитуды будут у 3, 6, 9, 12, ….гармоник.

С увеличением скважности «первый нуль» смещается в область гармоник с большими номерами и, следовательно, скорость убывания амплитуд гармоник уменьшается. Простой расчет амплитуды первой гармоники при U_m=100В для скважности S=2, U _m ₁=63,7B, при S=5, U _m ₁=37,4B и при S=10, U _m ₁=19,7B, т.е. с ростом скважности амплитуда первой гармоники резко уменьшается. Если же найти отношение амплитуды, например, 5-й гармоники U _m ₅ к амплитуде первой гармоники U _m ₁, то для S=2, U _m ₅/U_m ₁=0,2, а для S=10, U _m ₅ / U_m ₁ =0,9, т.е. скорость затухания высших гармоник с ростом скважности уменьшается.

Таким образом, с ростом скважности спектр последовательности прямоугольных импульсов становится более равномерным.

2.5. Спектры при уменьшении длительности импульса и периода сигнала.

Регулировать скважность S = T / t_n можно либо изменением длительности импульса t_n при T=const, либо изменением периода Т при t_n=const. Рассмотрим спектры сигналов при этом.

1. T=const, t_n=var. Частота первой гармоники f ₁ =1/ T =const и D f = f ₁ =const. Первый нуль N = T / t_n и по мере укорочения импульса t_n смещается в область гармоник с большими номерами. При t_n®0 N®¥, спектр получается дискретным и D f = f ₁, бесконечно широкий и с бесконечно малыми амплитудами гармоник.

2. t_n =const, T =var. Будем увеличивать период Т, тогда частота первой гармоники f ₁ и расстояние между спектральными линиями D f будут уменьшаться. Так как D f = f ₁ =1/Т, то спектральные линии будут смещаться в область более низких частот и «плотность» спектра возрастет. Если Т®¥, то сигнал из периодического становится непериодическим (одиночный импульс). В этом случае f ₁ = D f®0, т.е. спектр из дискретного превращается в непрерывный, состоящий из бесконечно большого числа спектральных линий, находящихся на бесконечно малых расстояниях друг от друга.

Отсюда следует правило: периодические сигналы порождают дискретные (линейчатые) спектры, а непериодические – сплошные (непрерывные).

При переходе от дискретного спектра к непрерывному ряд Фурье заменяется интегралом Фурье. Наиболее просто эта замена выполняется, если использовать запись ряда Фурье в комплексной форме (16) и (17). Интеграл Фурье для непрерывного спектра записывается

, (30)

где (31)

Функция F ( j w ) называется спектральной функцией или спектральной плотностью, которая зависит от частоты. Формулы (30) и (31) называют в совокупности односторонним преобразованием Фурье, которое является частным случаем более общего преобразования Лапласа и получается заменой в преобразовании Лапласа комплексной переменной р на j w .

Спектральную функцию можно представить как огибающую коэффициентов ряда Фурье, т.е. как предел линейчатого спектра периодической функции при Т®¥. Функция F ( j w ) может быть действительной или комплексной. Считая в общем случае , мы получаем две частотные характеристики: - амплитудный спектр, т.е. зависимость амплитуды спектральных составляющих от частоты, и y ( w ) – фазовый спектр, т.е. закон изменения фазы спектральных составляющих сигнала от частоты. Можно показать, что амплитудный спектр – всегда четная, а фазовый спектр – всегда нечетная функция w . Спектральную функцию для многих непериодических сигналов (одиночных импульсов различной формы) наиболее легко и просто находить с помощью таблиц оригиналов и изображений в преобразовании Лапласа, которые приводятся в учебной и справочной литературе. После нахождения изображения по Лапласу F ( p ) для заданной непериодической функции f ( t ), спектральная функция находится

(32)

Итак, согласно (30) непериодическая функция f ( t ) представляется совокупностью бесконечно большого числа гармоник с бесконечно малыми амплитудами во всем диапазоне частот от - ¥ до +¥, т.е. представление f ( t ) в виде интеграла Фурье подразумевает суммирование незатухающих гармонических колебаний бесконечного сплошного спектра частот.

3. описание лабораторной установки

Работа выполняется на блоке «Синтезатор сигнала», функциональная схема которого приведена на рис. 16.

Блок содержит генераторов Г1-Г6 шести первых гармоник сигнала. Частота первой гармоники равна 10 кГц. Гармонический сигнал с выхода n-го генератора через фазовращатель Ф_n и аттенюатор А_n поступает на сумматор. Фазовращателями задают начальные фазы j_n гармоник, а аттенюаторами – их амплитуды А_n.

«синхр»

Рис. 16

На выходе сумматора в общем случае получается сумма шести гармоник сигнала

С выхода сумматора сигнал подается на вход Y осциллографа. Для его внешней синхронизации используется специальный импульсный сигнал, подаваемый с гнезда «Синхр.» на вход Х осциллографа. Для установки и контроля амплитуд гармоник предусмотрена возможность отключения любой из гармоник. Включив только генератор n-ой гармоники, можно установить ее амплитуду аттенюатором А_n и оценить ее значения с помощью осциллографа. Каждый фазовращатель с помощью переключателя позволяет установить требуемое дискретное значение начальной фазы гармоники, либо отключить генератор.

4. Расчетная часть. (выполняется при домашней подготовке)

Для приведенных в теоретической части сигналов рассчитать амплитудный спектр An и фазовый спектр j _n для шести низших гармоник. Амплитуду первой гармоники принять равной 5В. Обратите внимание, что амплитуды гармоник An-неотрицательны, а возникающие в расчетах знаки «минус» следует отнести к фазе гармоники. Результаты расчетов для каждого сигнала необходимо свести в таблицу. Необходимые для расчетов параметры сигналов заданы в таблице 1.

n	1	2	3	4	5	6
An, B	5
j _n, град

Таблица 1.

Номер стенда	1	2	3	4	5	6
Т/ t _j	7	8	4	4,5	5	6
Q	3	4	5	6	7	8
M	1	0,9	0,8	0,7	0,6	0,5

Здесь t _j -длительность фронта сигнала (рис. 9), Т - его период, Q – скважность последовательности импульсов (рис. 11), М - индекс амплитудной модуляции сигнала (26^’).

Внимание!Выполнение лабораторной работы без полностью восполненной расчетной части невозможно, поэтому студенты, не выполнившие задание, к лабораторной работе не допускаются.

5. Экспериментальная часть.

5.1.Подключить вход Y осциллографа к гнёздам «Выход», а вход Х - к гнезду «Синхр.». Установить внешнюю синхронизацию осциллографа.

5.2. Установить все переключатели Фn в положение «Выкл», а переключатели DФ₃ и DФ₅ - в положении «О». При этом сигнал на выходе сумматора должен отсутствовать.

5.3. Установить требуемые амплитуды гармоник для сигнала п.2.2, а).

5.3.1.Установить переключатель Ф1 в положение «О».Потенциометром А1 установить требуемую амплитуду первой гармоники на выходе сумматора. Вернуть переключатель Ф₁ в положение «Выкл».

5.3.2. Выполнить эту же операцию для всех остальных гармоник выбранного сигнала.

5.4. Переключателями Фn установить требуемый фазовый спектр сигнала. Зарисовать осциллограмму полученного на экране сигнала.

5.5. Зарисовать осциллограммы сигнала при всех положениях переключателя DФ₃.Сделать вывод об искажениях сигнала, обусловленных погрешностями установки фазового спектра сигнала. Вернуть переключатель DФ₃ в положение «О».

5.6. Повторить пункты 5.3 и 5.4 для всех представленных теоретической части сигналов п.2.2 (б-з).

6. Содержание отчета.

6.1. Расчеты и таблицы амплитуд и фаз шести гармоник, графики амплитудных и фазовых спектров всех синтезируемых сигналов.

6.2. Экспериментальные осциллограммы всех сигналов.

6.3. Анализ полученных результатов и выводы по работе.

7. Контрольные вопросы.

7.1. Какие функции называются ортогональными? Приведите примеры.

7.2. Что собой представляет ряд Фурье?

7.3. Как вычисляются коэффициенты обобщенного ряда Фурье?

7.4. Запишите ряд Фурье в комплексной форме и определите его

коэффициенты.

7.5. Запишите ряд Фурье в тригонометрической форме. Укажите связь между коэффициентами ряда Фурье при различных формах его записи.

7.5. Дать определение и привести примеры амплитудных и фазовых

спектров сигналов.

7.7. Нарисуйте амплитудные спектры меандра и последовательности прямоугольных импульсов при различных значениях скважности. Укажите их отличия.

7.8. Что собой представляет интеграл Фурье. В каких случаях он применим.

7.9. Что характеризует спектральная характеристика сигнала.

7.10 Что собой представляют амплитудный и фазовый спектр непериодического сигнала.

7.11. Запишите аналитическое выражение АМ-сигнала.

7.12. Как выглядит спектр АМ-сигнала при гармоническом модулирующем сигнале.

7.13. При каких условиях АМ- колебание можно отнести к периодическим сигналам.

8. Литература.

1. Басков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа,2000.

2. Матханов П.Н. Основы синтеза линейных электрических цепей. – М.: Высшая школа,1976.

3. Гоноровский И.С. Радиотехнические цепи и сигналы. – М.: Радио и связь,1978.

4. Атабеков Г.И. Теоретические основы электротехники,4.1 –М.: Энергия, 1978.

Дата добавления: 2018-11-24; просмотров: 1021; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!