Симплекс-метод решения задач линейного программирования с n -переменными
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Ижевский государственный технический университет имени М.Т.Калашникова»
Институт «Современные технологии машиностроения , автомобилестроения и металлургии»
Кафедра «Конструкторско-технологическая подготовка машиностроительных производств»
Работа защищена с оценкой
«_______________________»
Дата_________________
Подпись____________/__________________
КУРСОВАЯ РАБОТА
по дисциплине «Математическое моделирование в машиностроении»
Вариант 2
Выполнил
Студент гр. Б05-721-3зтА.С.Клековкина
Руководитель
Старший преподаватель кафедры КТПМП Е.В.Королёва
Рецензия:
степень достижения поставленной цели работы__________________________________
полнота разработки темы_____________________________________________________
уровень самостоятельности работы обучающегося________________________________
недостатки работы___________________________________________________________
___________________________________________________________________________
Ижевск 2018
Содержание
Содержание. 2
Введение. 3
1. Задачи линейного программирования. 4
2.Постановка и решение задачи. 11
3.Анализ решения задачи и оптимизация производства. 20
Заключение. 26
Список литературы.. 27
Введение
Цель курсовой работы - теоретическое освоение математических моделей вопросах оптимального распределения ресурсов производства и практическая реализация одной из задач обозначенного класса с помощью математического пакета Excel.
|
|
|
Задачи курсовой работы:
- изучить учебную и научную литературу об использовании математических моделей для решения производственных задач, в том числе в машиностроении;
- освоить основы выбора математических моделей для представления задач планирования производства, составления математической модели задачи;
- постановка и решение задачи оптимизации производственного плана, поиск решения ее в среде Excel;
- закрепление навыков формулировки предложений по изменению параметров модели с целью улучшения критериальной функции.
Задачи линейного программирования
Методы математического программирования представляют собой класс моделей, применяемых для формализации задач планирования, предусматривающих распределение ограниченного количества ресурсов разных видов. Подобного рода задачи решаются в различных отраслях деятельности: в экономике, в различных отраслях промышленности, при разработке проектов, составлении расписаний, планировании военных операций и т. п.
|
|
|
Употребление слова «программирование» в данном отношении связано с тем, что при решении задач находят такой набор переменных, который является программой (планом) при выполнении поставленной задачи. Методы линейного программирования применяются в случае, когда математическая модель изучаемого процесса может быть представлена в виде совокупности линейных отношений. Эти линейные отношения связывают некоторые параметры, определяющие ход процесса, и состоят из системы ограничений и целевой функции.
Методы решения такого типа задач позволяют найти оптимальные варианты управления, процессы, структуры, т. е. выбрать лучшее решение из всех возможных. Такие задачи относятся к задачам оптимизации.
Условно типы задач из области машиностроения можно разделить на:
- технико-экономические;
- технические;
- технологические;
- проектно-организационные;
- транспортные.
Косвенным образом соотносятся с машиностроением и другие типы задач, которые могут быть решены методом линейного программирования: задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса и аналогичные им.
В рассматриваемой курсовой работе требуется составить математическую модель задачи машиностроения, основанной на линейном программировании. Поставлена задача увеличения дохода предприятия при одновременной экономии ресурсов и решить ее с помощью надстройки Поиск решения пакета Excel. Такие задачи относят к задачам линейного программирования.
|
|
|
В современной науке и технике особенно велика роль моделей. Чем более сложным и надежным должно быть техническое изделие, тем большее число моделей потребуется на этапе его проектирования.
Под моделью (от лат. modulus – мера, образец, норма) понимают такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект - оригинал, сохраняя некоторые важные для данного исследования типичные его черты. Процесс построения и использования модели называется моделированием.
Модель - это физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта.
Модель - инструмент, ориентированный, в первую очередь, на исследование поведения и свойств конкретного объекта (или характеристик конкретного процесса) в целях управления им или предсказания его параметров и режимов функционирования.[1]
|
|
|
Линейное программирование – это метод оптимизации моделей, в которых целевые функции и ограничения строго линейны. Линейное программирование успешно применяется в военной области, индустрии, сельском хозяйстве, транспортной отрасли, экономике, системе здравоохранения и даже в социальных науках. Широкое использование этого метода также подкрепляется высокоэффективными компьютерными алгоритмами, реализующими этот метод.
На алгоритмах линейного программирования (учитывая их компьютерную эффективность) базируются оптимизационные алгоритмы для других, более сложных типов моделей и задач исследования операций, включая целочисленное, нелинейное и стохастическое программирование. [2]
Линейное программирование – направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейной зависимостью между переменным и линейным критерием оптимальности.
К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.
Круг задач, решаемых при помощи методов линейного программирования достаточно широк. Например:
- задача об оптимальном использовании ресурсов при производственном планировании;
- задача о смесях (планирование состава продукции);
-задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах (управление товарно-материальными запасами или «задача о рюкзаке»);
-транспортные задачи (анализ размещения предприятия, перемещение грузов).
Линейное программирование – наиболее разработанный и широко применяемый раздел математического программирования (кроме того, сюда относят: целочисленное, динамическое, нелинейное, параметрическое программирование). Это можно объяснить следующими причинами:
- математические модели большого числа экономических задач линейны относительно искомых переменных;
- данный тип задач в настоящее время наиболее изучен. Для него разработаны специальные методы, с помощью которых эти задачи решаются, и соответствующие программы для ЭВМ;
- многие задачи линейного программирования, будучи решенными, нашли широкое применение;
- некоторые задачи, которые в первоначальной формулировке не являются линейными, после ряда дополнительных ограничений и допущений могут стать линейными или могут быть приведены к такой форме, что их можно решать методами линейного программирования.
Экономико-математическая модель любой задачи линейного программирования включает:
целевую функцию, оптимальное значение которой (максимум или минимум) требуется отыскать;
систему ограниченийв виде системы линейных уравнений или неравенств;
условие неотрицательности переменных.
Задача линейного программирования называется канонической, если ограничения задачи состоят из системы уравнений и условий неотрицательности всех n переменных.
Каноническая задача записывается в виде
 ,
,
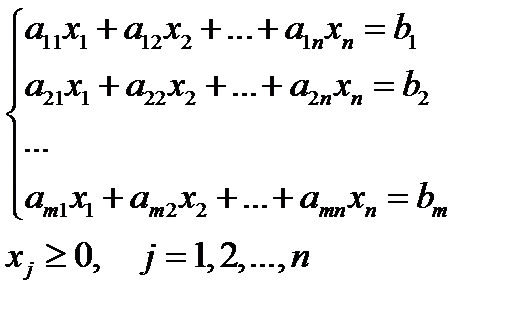
Задача линейного программирования называется симметрической, если она имеет вид
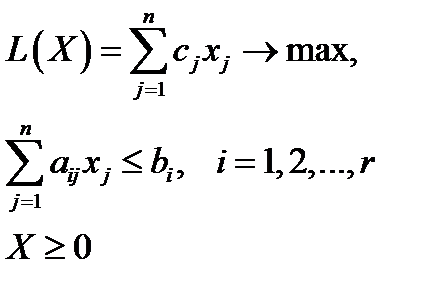
 или
или
Общая задача линейного программирования может быть приведена к каноническому виду при помощи следующих утверждений:
1. Неравенство

равносильно равенству

и простейшему неравенству

2. Неравенство

равносильно равенству

и простейшему неравенству

3. Каждую переменную, на которую не наложено условие отрицательности, можно представить в виде разности двух неотрицательных переменных

Сформулированные задачи представляют собой линейные математические модели общих задач оптимизации, которые заключаются в нахождении в заданной области точек наибольшего и наименьшего значения некоторой линейной функции, зависящей от большого числа переменных. Такие задачи возникают в самых разнообразных областях человеческой деятельности, главным образом в практике планирования и организации производства.
В настоящее время разработаны различные способы решения задач линейного программирования. При небольших размерностях возможно осуществить их ручной просчет, при больших на помощь в решении приходит компьютер.
Различают следующие типы линейных оптимизационных задач:[4]
- задачи о перевозках, например, минимизация расходов по доставке товаров с нескольких фабрик в несколько магазинов с учетом спроса;
- задачи распределения рабочих мест, например, минимизация расходов на содержание штата с соблюдением требований, определенных законодательством;
- управление ассортиментом товаров: извлечение максимальной прибыли с помощью варьирования ассортиментным набором товаров (при соблюдении требований клиентов). Аналогичная задача возникает при продаже товаров с разной структурой затрат, рентабельностью и показателями спроса;
- замена или смешивание материалов, например, манипуляция материалами с целью снижения себестоимости, поддержания необходимого уровня качества и соблюдения требований потребителей;
- -задача о диете. Из имеющихся в распоряжении продуктов требуется составить такую диету, которая, с одной стороны, удовлетворяла бы минимальным потребностям организма в питательных веществах (белки, жиры, углеводы, минеральные соли, витамины), с другой — требовала бы наименьших затрат;
- задача распределения ресурсов, например, распределение ресурсов между работами таким образом, чтобы максимизировать прибыль, или минимизировать затраты, или определить такой состав работ, который можно выполнить, используя имеющиеся ресурсы, и при этом достичь максимума определенной меры эффективности, или рассчитать, какие ресурсы необходимы для того, чтобы выполнить заданные работы с наименьшими издержками.
Задача линейного программирования может:
- иметь единственное решение;
- иметь бесчисленное множество решений;
- не иметь решения (из-за несовместности системы ограничений или из-за неограниченности целевой функции на множестве планов).
Перечислим обзорно известные методы решения задач линейного программирования: [5],[6]
- графический метод (применяется в случае, если задача содержит два (реже – три) неизвестных;
- симплекс-метод (универсальный способ, может применяться для решения практически любых задач линейного программирования);
- метод искусственного базиса;
- методы целочисленного линейного программирования (метод ветвей и границ, метод отсечения Гомори).
Симплекс-метод решения задач линейного программирования с n -переменными
«Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Этот метод является универсальным, применимым к любой задаче линейного программирования в канонической форме. Система ограничений здесь — система линейных уравнений, в которой количество неизвестных больше количества уравнений. Если ранг системы равен r, то мы можем выбрать r неизвестных, которые выразим через остальные неизвестные. Для определенности предположим, что выбраны первые, идущие подряд, неизвестные x1 , x2 , ..., xr .
Правда, не всегда можно выражать через остальные первые r неизвестных (мы это сделали для определенности записи). Однако такие r неизвестных обязательно найдутся. Эти неизвестные (переменные) называются базисными, остальные свободными.
Придавая определенные значения свободным переменным и вычисляя значения базисных (выраженных через свободные), мы будем получать различные решения нашей системы ограничений. Таким образом, можно получить любое ее решение. Нас будут интересовать особые решения, получаемые в случае, когда свободные переменные равны нулю. Такие решения называются базисными, их столько же, сколько различных базисных видов у данной системы ограничений. Базисное решение называется допустимым базисным решением или опорным решением, если в нем значения переменных неотрицательны. Если в качестве базисных взяты переменные x1 , x2 , ..., xr , то решение {b1 , b2 ,..., br , 0, ..., 0} будет опорным при условии, что b1 , b2 ,..., br ≥ 0.
Симплекс-метод основан на теореме, которая называется фундаментальной теоремой симплекс-метода. Среди оптимальных планов задачи линейного программирования в канонической форме обязательно есть опорное решение ее системы ограничений. Если оптимальный план задачи единственен, то он совпадает с некоторым опорным решением. Различных опорных решений системы ограничений конечное число. Поэтому решение задачи в канонической форме можно было бы искать перебором опорных решений и выбором среди них того, для которого значение F самое большое. Но, во-первых, все опорные решения неизвестны и их нужно находить, a, во-вторых, в реальных задачах этих решений очень много и прямой перебор вряд ли возможен. Симплекс-метод представляет собой некоторую процедуру направленного перебора опорных решений. Исходя из некоторого, найденного заранее опорного решения по определенному алгоритму симплекс-метода мы подсчитываем новое опорное решение, на котором значение целевой функции F не меньше, чем на старом. После ряда шагов мы приходим к опорному решению, которое является оптимальным планом.
Итак, симплексный метод вносит определенный порядок как при нахождении первого (исходного) базисного решения, так и при переходе к другим базисным решениям. Его идея состоит в следующем.
Имея систему ограничений, приведенную к общему виду, то есть к системе m-линейных уравнений с n-переменными (m < n), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще.
Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то, осуществляется переход к другому, обязательно допустимому базисному решению.
Симплексный метод гарантирует, что при этом новом решении линейная форма, если и не достигнет оптимума, то приблизится к нему. С новым допустимым базисным решением поступают так же, пока не находят решение, которое является оптимальным.
Если первое найденное базисное решение окажется недопустимым, то с помощью симплексного метода осуществляется переход к другим базисным решениям, которые приближают нас к области допустимых решений, пока на каком-то шаге решения либо базисное решение окажется допустимым и к нему применяют алгоритм симплексного метода, либо мы убеждаемся в противоречивости системы ограничений.
Таким образом, применение симплексного метода распадается на два этапа: нахождение допустимого базисного решения системы ограничений или установление факта ее несовместности; нахождение оптимального решения.
При этом каждый этап может включать несколько шагов, соответствующих тому или иному базисному решению. Но так как число базисных решений всегда ограниченно, то ограниченно и число шагов симплексного метода» [7].
Постановка и решение задачи
Производственная фирма производит 3 вида продукции: Р1,Р2,Р3. Доход на единицу каждого вида продукции Р1, Р2 и Р3 известен: 300, 240 и 400 руб. соответственно.
Также известно, что
1) При производстве используются материалы М1 и М2, ежедневные запасы которых не превышают заданных значений. Расход материалов на каждое изделие известен: по М1 - м11, 2, 1 соответственно, по М2 -1, 1, 1.
2) Материалы обрабатываются на станках С1 и С2, ежедневное время работы которых ограничено. На станке С1 обрабатывается каждое изделие Р1,Р2 в течение 1 мин и Р3 в течение р3 мин. На станке С2 – только изделие Р1 в течение 1 мин и изделие Р3 в течение 4 мин.
3) Ежедневный объем производства изделия Р2 ограничен.
4) При планировании выпуска учесть расход инструмента до полной его замены, который задан в процентах износа на единицу продукции. Расход инструмента зависит от выбранной скорости резания. Так, для принятой на производстве скорости резания расход составляет 7%, 3% и 5% на 1 шт. изделий соответственно.
5) Числовые данные приведены в таблице 1 по вариантам.
На предприятии разрабатывается Стратегия повышения эффективности производства и управления. Рассмотреть ряд предложений-мероприятий на предмет их включения в Стратегию:
1. Увеличить на 20% доход от Р3 с одновременным снижением его объема выпуска на 10%.
2. Приобрести дополнительные объемы любого одного материала у сторонних поставщиков, цена у которых на 5% выше, чем нынешняя для основного объема материала.
3. Увеличить минимальный объем производства продукта Р2 на 10%.
4. Увеличить в 2 раза скорость резания. В 2 раза сократится время обработки изделий, но расход инструмента вырастет в 3 раза.
Определить, к каким результатам приведет внедрение каждого из предложений Стратегии. Дать развернутое пояснение, проверить предложения на совместимость. Предложить собственное мероприятие и доказать его целесообразность.
Задание:
М1=480
м11=1
М2=390
И1=70
С1=380
р3=2
С2=470
Объем производства Р2≥80
Решение.
Для более наглядного представления условия задачи представим исходные данные в виде таблицы.
| Изделия Ресурсы | Вид продукции | Запас | ||
| Р1 | Р2 | Р3 | ||
| М1 | 1 | 2 | 1 | 480 |
| М2 | 1 | 1 | 1 | 390 |
| С1 | 1 | 1 | 1 | 360 |
| С2 | 1 | 0 | 4 | 470 |
| Расход инструмента | 0,07 | 0,03 | 0,05 | 70 |
| Ограничения | ³80 | |||
| Доход | 300 | 240 | 400 | |
Данная задача является задачей линейного программирования по максимизации прибыли при имеющихся ограничениях ресурсов.
Опишем математическую модель задачи.
Обозначим:
 - план выпуска изделия Р1,
- план выпуска изделия Р1,
 - план выпуска изделия Р2,
- план выпуска изделия Р2,
 - план выпуска изделия Р3.
- план выпуска изделия Р3.
Тогда целевую функцию задачи можно сформулировать следующим образом:
Т.к. цель предприятия – максимизация дохода, то целевая функция:

Известно, что при производстве используются материалы М1 и М2, ежедневные запасы которых не превышают значений 480 и 390 соответственно.
Расход материалов на каждое изделие известен: по М1 - 2, 2, 1 соответственно, по М2 -1, 1, 1.
Из этих данных получаем ограничения по используемым материалам:

Известно, что материалы обрабатываются на станках С1 и С2, ежедневное время работы которых ограничено 360 и 470 мин соответственно. На станке С1 обрабатывается каждое изделие Р1,Р2, Р3 в течение 1 мин. На станке С2 –только изделие Р1 в течение 1 мин и изделие Р3 в течение 4 мин.
Получаем ограничения по времени обработки:

Т.к. ежедневный объем производства изделия Р2 ограничен и должен составлять не менее 80 единиц, получаем ограничение:

Учтем расход инструмента до полной его замены, который задан в процентах износа на единицу продукции. Значит оборудование заменяется если его износ составит 100%. Для принятой на производстве скорости резания расход составляет 7%, 3% и 5% на 1 шт. изделий соответственно.
Поэтому ограничение по расходу инструмента:

Очевидно, что количество выпускаемых изделий не может быть отрицательным числом или дробным числом, поэтому


Получена математическая модель задачи:








Система ограничений задачи имеет вид:

при условии неотрицательности всех входящих в допустимый план переменных

Найдем решение задачи в среде Excel с помощью надстройки Поиск решения.
Подготовим исходную информацию и формулы на листе Excel.

Рисунок 1- Окно с введенными формулами
Для подбора оптимальных значений переменных  выделим диапазон ячеек B13:D13.
выделим диапазон ячеек B13:D13.
Для значения целевой функции выделим ячейку B16.
В ячейку для целевой функции B1 запишем формулу:
=СУММПРОИЗВ(B13:D13;B9:D9)
Для ограничений выделим диапазон H3:J8.
Вызовем и настроим Поиск решения.

Выполним поиск решения.Решение найдено:
Т.е. при заданных ограничениях оптимальный план выпуска продукции должен составлять 300 единиц продукции Р1 и 80 единиц продукции Р2.
При этом доход составляет 109200 руб.
Сохраним все доступные виды отчетов:
- отчет по результатам,
- отчет по устойчивости
- отчет по пределам.
Полученный результат:
Максимальный доход в размере 109200 руб. может быть получен при реализации следующего оптимального плана:
300 изделий вида Р1 и 80 изделий вида Р2.
Значение целевой функции  2
2  0
0
Изделия вида Р3 при имеющихся ограничениях выпускать нерентабельно.
Все ограничения задачи выполнены.
С точки зрения расхода ресурсов имеем:
- Материалы М1, М2 не является дефицитным ресурсом, он использован не полностью. Оставшуюся разницу (480–460 =20 кг, 390-380 =20 кг) можно реализовать сторонним организациям, тем самым увеличив доход.
- Время работы на станке С1 дефицитный ресурс, оно использовано полностью.
- Время работы на станке С2 не является дефицитным ресурсом, осталось в запасе 470 – 300 = 170 мин. В это время станок можно занять выполнением другой задачи или сдать в аренду сторонней организации.
Дата добавления: 2018-05-01; просмотров: 1558; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
