Расстояние от точки до прямой
Дано: прямая lзадана нормальным уравнением в векторной форме 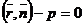


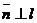 Требуется найти расстояние от точки до прямой.
Требуется найти расстояние от точки до прямой.
Возможны 2 случая:
1. т. М0 и начало координат лежат по разные стороны от прямой
2. т. М0и начало координат лежат по одну сторону от прямой
Рассмотрим 1 случай.
 соединим
соединим 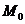 и 0
и 0  - радиус вектор точки М0
- радиус вектор точки М0
Опустим из точки 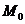 перпендикуляр на l,обозначим точкой K(x,y)
перпендикуляр на l,обозначим точкой K(x,y)
 - расстояние от точки до прямой. Соединим точкуО с точкойK, получим
- расстояние от точки до прямой. Соединим точкуО с точкойK, получим  - радиус-вектор точки К.
- радиус-вектор точки К.
Из треугольника ОМ0К видно, что
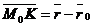 с одной стороны, а с другой стороны
с одной стороны, а с другой стороны 
 , а так как точка Кпринадлежит l, значит, координаты ее радиус вектора координаты удовлетворяют уравнению
, а так как точка Кпринадлежит l, значит, координаты ее радиус вектора координаты удовлетворяют уравнению  подставляем и получаем
подставляем и получаем  по свойству скалярного произведения
по свойству скалярного произведения  , отсюда
, отсюда  - расстояние от точки до прямой
- расстояние от точки до прямой
Во втором случае 




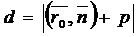 - общий случай
- общий случай


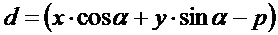 - расстояние от точки до прямой в координатной форме.
- расстояние от точки до прямой в координатной форме.
 -отклонение точки от прямой
-отклонение точки от прямой
Если Δ>0, то 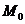 и 0 лежат по разные стороны от прямой
и 0 лежат по разные стороны от прямой
Если Δ<0, то по одну сторону от прямой
Вывод.: чтобы найти расстояние от точки до прямой, нужно уравнение привести к нормальному виду и подставить вместо х и у координаты заданной точки.
Пр.:  12х+15у+9=0
12х+15у+9=0

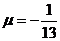

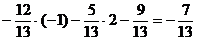

Каноническое уравнение прямой.
Параметрическое уравнение прямой.
Дано: прямая l, такая что  ,
, 
 ,
, 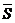 - направляющий вектор прямой l, возьмем произвольную точку M на прямой l и рассмотрим
- направляющий вектор прямой l, возьмем произвольную точку M на прямой l и рассмотрим 
 ,так как
,так как  ,то
,то  и коллинеарные, следовательно их коэффициенты пропорциональны.
и коллинеарные, следовательно их коэффициенты пропорциональны.
 - каноническое уравнение прямой
- каноническое уравнение прямой
 - параметрическое уравнение прямой, t – параметр.
- параметрическое уравнение прямой, t – параметр.
Уравнение прямой проходящей через две заданные точки
Дано: прямая l, 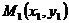 и
и 
 Возьмем точку
Возьмем точку  и рассмотрим два вектора
и рассмотрим два вектора  и
и  - эти вектора коллинеарны, следовательно коэффициенты пропорциональны
- эти вектора коллинеарны, следовательно коэффициенты пропорциональны
 - уравнение прямой проходящей через две заданные точки
- уравнение прямой проходящей через две заданные точки
Уравнение прямой с угловым коэффициентом

 - угловой коэффициент
- угловой коэффициент
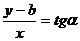
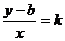
 -уравнение прямой с угловым коэффициентом
-уравнение прямой с угловым коэффициентом
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Возьмем  (1), и т.к. точка
(1), и т.к. точка  , то ее координаты удовлетворяют уравнению прямой:
, то ее координаты удовлетворяют уравнению прямой:  (2), из (2) вычтем (1), получаем:
(2), из (2) вычтем (1), получаем:  - уравнение прямой, проходящей через заданную точку.
- уравнение прямой, проходящей через заданную точку.
Угол между двумя прямыми

 и
и  - угловой коэффициент
- угловой коэффициент


так как  - внешний угол, то
- внешний угол, то

Условие параллельности двух прямых
 =0
=0 
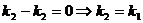 -условие параллельности прямых
-условие параллельности прямых
Условие перпендикулярности двух прямых



 -условие перпендикулярности двух прямых
-условие перпендикулярности двух прямых
Уравнение пучка прямых
Дано: две пересекающиеся прямые 1:  , пусть т. М0 (x0, y0)точка пересечения, тогда
, пусть т. М0 (x0, y0)точка пересечения, тогда  (*)
(*)
Первое уравнение умножим на  , второе – на
, второе – на  и сложим:
и сложим:
 - это уравнение определяет прямую Покажем, что она проходит через точку М0 (x0, y0):
- это уравнение определяет прямую Покажем, что она проходит через точку М0 (x0, y0):
 - см. (*).
- см. (*).
Таким образом, 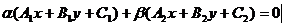 - уравнение пучка прямых.
- уравнение пучка прямых.
Разделим обе части на  :
:


уравнение пучка прямых - 
Дата добавления: 2018-02-28; просмотров: 331; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
