Числовые последовательности с конечными разностями

Г. Обнинск, 2011

Предисловие

Сложение – по сути, основная операция математики, которая отражает реальную картину природных процессов. Сегодня, живя в век электронно-вычислительных машин, мы редко задумываемся над операцией сложения чисел, хотя, несомненно, замечаем, что чуть ли не каждая задача, иногда очень необычная, приводит именно к нему. На первый взгляд, кажется, что сложение это просто, но очень часто эта простота обманчива. Конечно, каждый знает, что 1+2=3; 1+2+3=6, а как же быть с 1+2+3+…+100=? Можно конечно сложить все эти сто чисел, но, что если их будет больше? Тем не менее, очень часто задачи, возникающие в процессе познания мира, приводили человека, к простому сложению, но такому сложению, которое он произвести обычным способом уже не мог. Что уже говорить о задачах, в которых приходится складывать бесконечное количество чисел? Подобное действие не может совершить ни один современный компьютер, даже, имея в своём распоряжении неограниченный запас времени. Очень интересна, в этой связи, проблема нахождения сумм рядов, которая привлекала внимание людей на протяжении столетий. Благодаря трудам таких великих математиков как Эйлер, Гаусс, Маклорен, были разработаны изящные методы решения подобных задач, значительно продвинувшие все области человеческого естествознания. Так, например, было найдено решение задачи о нахождении напряжённости поля бесконечной системы зарядов. Впервые её решил Леонард Эйлер, найдя сумму ряда .

Колоссальная важность этой темы и оригинальность методических подходов, применяемых в этой отрасли математики, вдохновили меня на написание данной работы, целью которой стало исследование некоторых вопросов теории конечных и бесконечных сумм.

В настоящем докладе представлены различные задачи, связанные с суммированием рядов, а так же найдены как частные, так и общие решения. В частности найдены формулы выражающие Д-зету функцию, как для чётных аргументов так и для произвольных, с конечным количеством членов где так же получены значения таких рядов как , а также 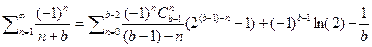и 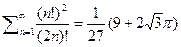и многие другие конечные и бесконечные суммы.

&1 Конечные суммы

Числовые последовательности с конечными разностями

№1 Разности

1) Основным объектом рассмотрения первой части работы являются последовательности чисел. Под последовательностью мы подразумеваем, совокупность упорядоченных чисел, каждому из которых ставится в соответствие его номер . Простейшей последовательностью является арифметическая прогрессия, к примеру: которая представляет просто ряд натуральных чисел. Очевидно, что номеру 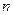в такой последовательности соответствует точно такой же элемент последовательности 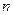. Но что если мы возьмём последовательность более сложного вида, например как видно её аналитическая форма , эту форму легко получить если заметить, что разность между соседними числами одна и та же, а значит, каждое последующее число получается из рекуррентного соотношения . Но как найти выражение 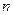-ного элемента в последовательности разность, в которой, соседних чисел различна, например: сразу видно, что разности между соседними числами не равны друг другу. Однако можно заметить, что полученные разности вновь образуют арифметическую прогрессию, то есть, одинаковы разности между соседними числами. Оказывается, что это свойство, сводится к постоянным разностям, имеют абсолютно все последовательности, стой лишь разницей, что зачастую приходить к этому они будут на бесконечном шаге нахождения разности между соседними числами. Но для последовательностей выраженных различными полиномами, как будет показано далее, всегда можно получить так называемые конечные (постоянные) разности, а найдя их можно будет построить формулу 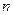-ного элемента последовательности.

2) Как мы видели ранее, основной характеристикой последовательностей является разности соседних элементов, а значит необходимо определить понятие первых, вторых и т.д. разностей и то, как они выражаются через элементы последовательности.Пусть у нас имеется числовая последовательность: y¹, y²,y³, y⁴,…: тогда первой разностью мы назовём величину Δy¹= y²- y¹, Δy²= y³- y², …; второй разностью Δ²y¹=Δ y²- Δy¹, Δ²y²=Δ y³- Δy², …; и вообще Δ^my¹=Δ^m-1 y²- Δ^m-1y¹. Далее непосредственно подстановкой убеждаемся, что Δ²y¹= y³-2y²+ y¹; Δ³y=y⁴-3y³+3y²- y¹;…

(1)

3) Теперь перейдём к решению основной задачи, а именно выражению 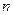-ного элемента последовательности через первые, вторые, и т.д. разности. Для этого воспользуемся неполной индукцией и предположением что -ные разности постоянны.Действительно пусть известны разности Δy, Δ²y, Δ³y, Δ⁴y,…, Δ^my,…; тогда положив Δ^my=Δ^my²= Δ^my³=…, получим, что:

а) Δ^m-1yⁿ= Δ^m-1y+(n-1)Δ^my

действительнобудем иметь Δ^m-1yⁿ⁺¹- Δ^m-1yⁿ=Δ^my; далее:

б) Δ^m-2yⁿ=Δ^m-2y+(n-1)Δ^m-1y+ Δ^my

поскольку Δ^m-2yⁿ⁺¹- Δ^m-2yⁿ= Δ^m-1y+ Δ^my= Δ^m-1y+(n-1)Δ^my и.т.д.

таким образом, получим, что:

в) yⁿ=y¹+(n-1)Δy+ Δ²y+ Δ³y+…

при этом мы полагаем n<=m так как в этом случае мы условно можем положить Δ^my=Δ^my¹=Δ^my²=… по причине того что коэффициенты (n-1)(n-2)(n-3)… при Δ^my, Δ^m+1y... равны нулю для n<=m. В итоге получим:

г) y^m=y¹+ (2)

4) Понятно, что задача поиска общего члена последовательности будет решена, если,

естественным образом, для некоторого m будет Δ^my=Δ^my²= Δ^my³=…, тогда для любого n

5) Подставив вместо Δy, Δ²y … их выражения через y¹, y² … будем иметь следующую формулу:

(4)

6) Очевидно, что если разности негде не становятся равными, то для получения формулы 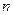-ного элемента последовательности потребуется 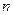разностей, а значит в этом случае задача не будет решена. Можно также отметить тот факт, что из вида формулы (3) можно сделать вывод, что любой элемент последовательности выражаемый некоторым монотонно возрастающим полиномами может быть выражен формулой(3) и для этого будет достаточно найти 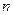разностей, если наибольшая степень выражения .

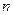№2 Сумма последовательности

1) Перейдём теперь к вопросу о суммировании последовательности, при этом будем считать, что последовательность образует конечные разности. Пусть снова имеется числовая последовательность: y¹, y²,y³, y⁴,… Тогда частными суммами мы назовём числа:

A¹=y¹;

A²=y¹+y²

A³= y¹+y²+y³

…

Очевидно, что A^m – сумма m членов предложенной последовательности. Найдём первые разности последовательности 0, A¹,A²,A³,… как видно они равны y¹, y²,y³,…à

Последовательность частных сумм имеет своей разностью саму исходную последовательность.

2) Если снова известны разности Δy, Δ²y, Δ³y, Δ⁴y,…, Δ^my,…; то задача нахождения суммы нечем не будет отличатся, от решаемой в предыдущем параграфе задачи о нахождении 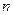-ного элемента последовательности, а значит сразу напишем, что сумма n членов последовательности будет равна:

3) Если известно m при котором Δ^my=Δ^my²= Δ^my³=… то произвольная сумма выразится через первые m+1 суммы:

(6)

№3 Тригонометрические последовательности

1) Преступим к нахождению суммы последовательности имеющей следующий вид:

2) Возьмём данную сумму и умножим и разделим её на , тогда получим, что преобразуем данное выражение

таким образом получим что теперь подробнее рассмотрим сумму мы вновь умноножим и разделим эту сумму на и получим, что продолжая совершать подобные действия получим следующее преобразование тригонометрической последовательности

3) Таким образом, нахождение суммы тригонометрических последовательностей свелось к вычислению разностей, но в отличии от ранее рассматриваемых задач помимо разности в данном случае требуется найти и разность , а значит для вычисления суммы потребуется найти формулу 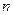-ного коэффициента