Достатня умова диференційовності функції двох змінних у точці
ЛЕКЦІЯ 22. Диференційовність функції двох змінних
ПЛАН
1. Частинні та повний прирости функції двох змінних
2. Диференційовність функції двох змінних
3. Достатня умова диференційовності функції двох змінних у точці
4. Диференціювання складної функції
5. Дотична площина та нормаль
6. Похідна за напрямом. Градієнт
7. Частинні похідні і повні диференціали вищих порядків
1. Частинні та повний прирости функції двох змінних
Нехай функція 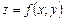 визначена в деякому околі точки
визначена в деякому околі точки  . Надамо незалежним змінним x та y приросту відповідно
. Надамо незалежним змінним x та y приросту відповідно  та
та  так, щоб точка
так, щоб точка  не виходила за межі вказаного околу. Тоді й точки
не виходила за межі вказаного околу. Тоді й точки  ,
,  також належатимуть розглядуваному околу (рис. 1).
також належатимуть розглядуваному околу (рис. 1).

Рис. 1
Означення 1. Різницю  називають повним приростом функції
називають повним приростом функції 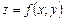 при переході від точки
при переході від точки  до точки
до точки  і позначають
і позначають  . Різницю
. Різницю  називають частинним приростом за х, а різницю
називають частинним приростом за х, а різницю  - частинним приростом за y функції
- частинним приростом за y функції 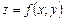 ; їх позначають відповідно
; їх позначають відповідно  і
і  . Таким чином,
. Таким чином,
 ,
,
 ,
,  .
.
Зауваження . Аналогічно визначаються прирости функції більш ніж двох змінних.
Диференційовність функції двох змінних
Означення 2. Функція 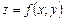 називається диференційовною у точці
називається диференційовною у точці  , якщо її повний приріст
, якщо її повний приріст  можна подати у вигляді:
можна подати у вигляді:
 ,
,
де А, В — числа, a, b — нескінченно малі при  .
.
Головна лінійна частина приросту функції, тобто  називається повним диференціалом функції (точніше першим диференціалом) двох змінних
називається повним диференціалом функції (точніше першим диференціалом) двох змінних  у точці
у точці  і позначається
і позначається 
|
|
|
 .
.
Теорема 1 . Якщо функція  диференційовна в точці
диференційовна в точці  , тоді існують границі
, тоді існують границі  та
та  і вони дорівнюють відповідно А і В.
і вони дорівнюють відповідно А і В.
Означення 3 . Нехай функція  визначена в точці
визначена в точці  і в її деякому околі. Якщо існує границя
і в її деякому околі. Якщо існує границя  , то вона називається частинною похідною за х (за у) функції
, то вона називається частинною похідною за х (за у) функції 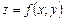 у точці
у точці  і позначається
і позначається 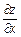 , або
, або  , або
, або  . Таким чином,
. Таким чином,  ,
,  . Із означення частинних похідних матимемо, що вони шукаються за тими правилами, що й похідні функції однієї змінної. Треба лише пам’ятати, що при знаходженні
. Із означення частинних похідних матимемо, що вони шукаються за тими правилами, що й похідні функції однієї змінної. Треба лише пам’ятати, що при знаходженні  у вважається сталою, а при знаходженні
у вважається сталою, а при знаходженні  змінна х вважається сталою.
змінна х вважається сталою.
Тепер можна сформулювати теорему 1 інакше:
Теорема 2 (необхідна умова диференційовності функції  у точці).
у точці).
Якщо функція  диференційовна в точці
диференційовна в точці  , то в цій точці існують частинні похідні
, то в цій точці існують частинні похідні  і
і  .
.
Приклад. Знайти 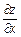 і
і  для функції
для функції 
 .
.
Знайдемо 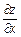 . Вважаючи, що
. Вважаючи, що  дістанемо:
дістанемо:
 .
.
При знаходженні  вважаємо, що
вважаємо, що  Дістанемо:
Дістанемо:
 .
.
Приклад. Знайти  і
і  для функції
для функції  .
.
Знайдемо  , вважаючи
, вважаючи 

Знайдемо  , вважаючи
, вважаючи 
 .
.
Приклад. Для функції  знайти
знайти  і
і  :
:
 ,
, 
Диференціали незалежних змінних збігаються з їхніми приростами:  ,
,  . Тоді, як випливає із означення повного диференціала і теореми 13, повний диференціал функції
. Тоді, як випливає із означення повного диференціала і теореми 13, повний диференціал функції 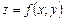 можна обчислити за формулою
можна обчислити за формулою
 .
.
|
|
|
Аналогічно повний диференціал функції трьох аргументів  обчислюється за формулою
обчислюється за формулою
 .
.
Приклад. Знайти  якщо
якщо  .
.
 ,
,  ,
,  .
.
Отже,  .
.
Приклад. Знайти  , якщо
, якщо  .
.
 , де
, де
 ;
;
 , отже,
, отже,
 .
.
Геометричний зміст частинних похідних. Якщо функцію 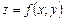 , що має частинні похідні в точці
, що має частинні похідні в точці  , розглядати за умови
, розглядати за умови  , то геометрично це означає, що поверхня
, то геометрично це означає, що поверхня 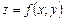 перетинається площиною
перетинається площиною  , паралельно координатній площині
, паралельно координатній площині  ; у перерізі дістаємо лінію. Тоді
; у перерізі дістаємо лінію. Тоді  є кутовим коефіцієнтом дотичної до зазначеного перерізу в точці
є кутовим коефіцієнтом дотичної до зазначеного перерізу в точці  , тобто тангенсом кута нахилу цієї дотичної до додатного напряму осі Ох. Аналогічно,
, тобто тангенсом кута нахилу цієї дотичної до додатного напряму осі Ох. Аналогічно,  є кутовим коефіцієнтом дотичної, що проходить через точку
є кутовим коефіцієнтом дотичної, що проходить через точку  , до кривої, яка утворюється в результаті перетину поверхні
, до кривої, яка утворюється в результаті перетину поверхні  з площиною
з площиною  .
.
Достатня умова диференційовності функції двох змінних у точці
Для функції однієї змінної твердження щодо її диференційовності та існування похідної є рівносильними. У випадку функції двох змінних ми маємо інше: існування частинних похідних - необхідна умова диференційовності функції в точці, але не є достатньою умовою диференційовності: наприклад, для функції

у точці (0; 0):  ,
,  . Але ця функція розривна в точці (0; 0), а тому функція не може бути диференційовною в цій точці. Таким чином, для диференційовності функції
. Але ця функція розривна в точці (0; 0), а тому функція не може бути диференційовною в цій точці. Таким чином, для диференційовності функції 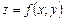 у точці
у точці  недостатньо тільки існування частинних похідних: потрібно додатково вимагати неперервності частинних похідних, що випливає з поданої далі теореми.
недостатньо тільки існування частинних похідних: потрібно додатково вимагати неперервності частинних похідних, що випливає з поданої далі теореми.
|
|
|
Теорема 3 . Якщо функція  у деякому околі точки
у деякому околі точки  має неперервні частинні похідні, тоді вона диференційовна в точці
має неперервні частинні похідні, тоді вона диференційовна в точці  .
.
Зауваження. Можна навести твердження про зв’язок між поняттями неперервності і диференційовності функції двох змінних у точці, аналогічні до тих, що виконуються для функції однієї змінної.
Теорема 3. Якщо функція  диференційовна в точці
диференційовна в точці  , то вона неперервна в цій точці. Обернене твердження неправильне.
, то вона неперервна в цій точці. Обернене твердження неправильне.
Дата добавления: 2022-01-22; просмотров: 18; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
