Примеры стратегий распределения ресурсов
Пример 6.1. Вновь вернемся к системе задач, информационный граф которой показан на рис. 1, а их априорные характеристики приведены в табл. 1. Положим, исходные данные те же, что и в примерах 4.1, 4.2 раздела 4 данной лекции. Необходимо при крайнем сроке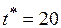 
построить стратегии распределения ресурсов, условно оптимальные по двум критериям – функции стоимости 
(2.6) и коэффициенту загрузки 
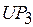(2.7) процессора третьего типа (заметим, что при сравнении двух альтернатив распределения при прочих равных условиях предпочтение отдается альтернативе с меньшим значением 
или большим значением 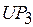). Для построения стратегии использовать обратную прогонку.
Построим стратегии, последовательно применяя оба критерия и уравнения (5.3) - (5.6). В табл. 2 варианты 1-6 представляют стратегию 
, условно оптимальную по 
, а варианты 7, 9, 11, 12, 14-17 соответствуют стратегии 
, условно оптимальной по 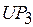. Напомним, что в соответствии с теоремой 3 в условно оптимальные стратегии попадают лишь те варианты распределения ресурсов, в которых коллизии разрешаются за счет процессоров тех же типов, что и базовые. В табл. 2 это – варианты 7, 9 и 12, в которых для разрешения коллизий вводится дополнительный процессор типа 3.
Стратегия строится с помощью процедур обратной прогонки и прямой раскрутки по уравнениям (5.3) - (5.5). Каждое значение длительности выполнения задачи 
(см. рис. 2) является условно оптимальным и определяет значение запаса по времени 
к началу запуска задачи 
. Так, при 
, а условно оптимальная длительность второй задачи равна 
. При этом 
и 
, 
. Условно оптимальные значения 
и 
рассчитываются по аналогии с тем, как это делается в примере 4.1. Для условно оптимальных длительностей 
по (5.6) находятся условно оптимальные назначения 
. Отношение 
, формируемое критерием , таково, что для любой альтернативы, не принадлежащей , значение функции стоимости не меньше, чем значение для любой из альтернатив в 
. При этом стратегия внутренне устойчива: в нее включаются варианты 1-7, каждый из которых является условно оптимальным по 
(см. табл. 2). При расчете коэффициента загрузки 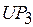берутся условно оптимальные длительности задач, использующих базовый процессор третьего типа.
|
|
|
Аналогично строится стратегия 
, условно оптимальная по критерию 
, с помощью которого формируется соответствующее отношение 
. Для любой из альтернатив, не входящей в , значение 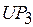не больше, чем значение этого критерия для любой из альтернатив из . Так же, как и , стратегия внутренне и внешне устойчива.
Положим, что 
и имеет место (5.2). Тогда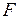 
-оптимальная стратегия совпадает с 
.
Пример 6.2 . Пусть для тех же исходных условий, что и примере 6.1, необходимо найти Парето-оптимальную стратегию распределения ресурсов, формируемую критериями и . И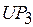спользовать обратную прогонку.
|
|
|
Очевидно, что отношение Парето представляет собой асимметричную часть отношения 
из примера 6.1. В табл. 2 Парето-оптимальная стратегия представлена вариантами 2, 3, 7, 12.
Соответствующие структуры вычислительной и коммуникационной сред показаны на рис. 5, а-г. Вариант 2 представляет распределение с минимальным значением функции стоимости (см. пример 4.1 и диаграмму на рис. 3).
Как уже говорилось, практически оправданным может быть ослабление требований к отношениям 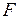и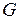 
. Так, 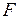-оптимальная стратегия, полученная в примере 6.1 и состоящая из 14 вариантов распределения ресурсов, охватывает больший диапазон временных параметров возможных контрольных событий в системе, чем Парето-оптимальная стратегия из четырех вариантов. Предположим, что фактическая динамика загрузки процессоров такова, что для задач 
(см. рис. 1 и табл. 2) может быть использовано не более пяти единиц времени при том же крайнем сроке 
завершения всех работ. Тогда из 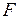-оптимальной стратегии может быть выбран любой из вариантов распределения ресурсов следующей совокупности: 1, ..., 6, 9, 11, 14, ..., 17. Кроме этого, стратегия может быть расширена за счет вариантов распределения, «близких» к оптимальным.
|
|
|
Рассмотрим следующий
Пример 6.3 . Положим, что условия примера 6.1 дополнены возможностью разрешения коллизий с помощью процессора, введение которого сопровождается минимумом штрафной функции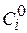 
. Как было показано в примере 4.2 раздела 4, это процессор четвертого типа. Коллизии между конкурирующими задачами (в вариантах 8 и 13 это 
, а в варианте 10 – 
) разрешаются за счет использования процессора именно этого типа (см. табл. 1 и 2). Диаграммы распределения ресурсов для вариантов 8 и 13 показаны на рис. 4, а и 4, в. В сравнении с вариантами 7, 9 и 12 это дает прирост значения в одну единицу стоимости.
Строго говоря, распределения 8, 10 и 13 не принадлежат оптимальной стратегии, поскольку функция стоимости должна рассчитываться по условно оптимальным значениям длительности. Однако, если определено понятие степени «близости» подобных вариантов к условно оптимальным, то они могут быть использованы для расширения стратегии. Так, в данном примере варианты 8, 13 ничем не уступают варианту 15, формально входящим в стратегию, условно оптимальную по критерию .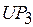
|
|
|
Заключение
1. В лекции изложен и обоснован подход к выбору состава (типов) и оптимизации распределения ресурсов в проблемно-ориентированных вычислительных системах, функционирующих в реальном времени.
2. Рассмотрены методы одно- и многокритериальной оптимизации распределения ресурсов, в основу которых положены аппараты динамического программирования и разрешения коллизий конкурирующих задач.
3. Разработанные методы позволяют формировать оптимальную стратегию, из которой может быть выбран конкретный вариант распределения ресурсов в зависимости от фактических временных параметров событий, наступающих в системе реального времени.
4. Нужно подчеркнуть, что непредсказуемость поведения окружения системы может быть причиной выбора неадекватной стратегии. Например, могут возникнуть такие отказы в системе, которые делают невозможным разрешение коллизий параллельных задач из-за отсутствия свободных процессоров. Однако это проблемы, требующие особого рассмотрения и выходящие за рамки данной лекции.
5. Наиболее целесообразным представляется применять предложенные методы в вычислительных системах с масштабируемой архитектурой.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1 . Обозначим через 
множество допустимых значений переменных 
, определяемых соответствующими диапазонами изменения 
. Рассмотрим конечные последовательности из 
элементов вида
,
где 
– векторы длительностей выполнения задач в соответствующих работах.
Множество таких последовательностей обозначим через 
. Последовательность 
является полной, если 
, 
. Выделим в 
подмножество 
полных последовательностей. В последовательности 
начальный отрезок 
и конечный отрезок 
назовем сопряженными.
Представим аддитивно-сепарабельный критерий 
(2.4) как монотонно-рекурсивный функционал, определенный на множестве 
:
(П.1) 
( 
)
,
где 
; 
– набор длительностей задач, соответствующих оптимальному планированию.
Последовательность 
или 
является оптимальной, если 
или 
.
Обозначим через 
множество полных допустимых последовательностей, начинающихся вектором 
, для которых 
является начальным отрезком. Пусть 
– множество всех конечных отрезков последовательностей множества 
, причем эти конечные отрезки являются сопряженными с 
.
Рассмотрим две допустимые последовательности 
такие, что имеет место 
. Это означает, что последовательность 
содержит меньше отрезков оптимального планирования для работ 
, чем последовательность 
. Это следует из свойства монотонной рекурсивности функционала 
(П.1). При этом очевидно, что 
, поскольку совокупность всех конечных допустимых отрезков, сопряженных с 
и 
, определяется диапазонами изменения переменных векторов 
независимо от их оптимальности. Тогда в соответствии с обобщенным принципом оптимальности динамического программирования последовательности множества 
не могут быть оптимальными. Это, в свою очередь, означает, что экстремум 
может быть достигнут тогда, когда 
, что и требовалось доказать.
Доказательство леммы. Введем обозначения: 
, 
. Предположим, что 
. Внешняя устойчивость 
исключает существование такой альтернативы 
распределения ресурсов. В общем случае 
. При этом
(П.2) 
.
Таким образом, из (П.2) следует
(П.3) 
.
Кроме этого,
(П.4) 
.
Следовательно, из (5.2), (П.3), (П.4) получаем, что
.
Теперь положим, что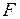 
антисимметрично. Благодаря внешней устойчивости 
и антисимметричности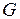 
, следующей из (5.2), имеет место:
(П.5) 
.
Поскольку внутренне устойчиво, то с учетом (П.5)
.
Лемма доказана.
РЕКОМЕДУЕМАЯ ЛИТЕРАТУРА
1. Топорков В.В. Модели распределенных вычислений. М.: Физматлит, 2004.
2. Таха Х. Введение в исследование операций: В 2 кн. М.: Мир, 1985.
3. Юдин Д.Б. Вычислительные методы теории принятия решений. М.: Наука, 1989.
4. Михалевич В.С., Кукса А.И. Методы последовательной оптимизации в дискретных сетевых задачах оптимального распределения ресурсов. М.: Наука, 1983.
Дата добавления: 2020-11-15; просмотров: 215; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!